

Abstract
This paper deals with procedural techniques of pattern generation. It describes evolutional textures, which are based on the cellular developmental models. Evolutional textures cover much of well-known texture generation techniques. Except of that, they are a strong base for creating a kind of random texture generator algorithm. I use cell programs for controlling their behaviour. These programs can be generated stochastically and system evolution can lead to complex pattern. Implementation for binary domain will be introduced. Creation of intuitively nice abstract pictures will be discussed. I made a language for helping texture developers to create interesting patterns. It is capable to simulate most of famous texture generation techniques.
Keywords: pattern generation, procedural textures, cellular systems, evolution.
1 Introduction
If someone, who is interested in graphics, wants to apply a natural-like pattern for the modeled virtual object, he needs some software offering a set of real images and/or controllable procedural textures. This software can be in the form of a package built into a rendering system or it can be a standalone application with possibility to export the results. No matter the form, its user interface is based on dividing the textures into the reasonable categories having specific features. Recently, an importance of procedural access grew. Therefore, more and more parameters for controlling the process of texture creation became needed. Graphician has to know much more about those categories and parameters than before. Layman could be lost.
Is there any easier way to input our requirements on the final pattern properties than setting a heap of numbers with not-so-clear interpretation? Imagine the optimal situation: user came to his computer, inputs a request like "narrow straight yellow stripes on the red fuzzy background", computer then asks him for the stripes direction and show five or six temporary results. User will have to choose the picture that best resembles his ideal and specify next requirements, e.g. "random distances between the stripes, smoother edges". After few steps he gets what he wanted. To develop such a smart application we need to know what may be considered as a good-looking abstract picture. We should define the borderline between nice abstract pictures and the others (trash) in the language of mathematics. Sounds like to describe the beauty of our world by group of equations. That is impossible. Despite of that, I will use the term "nice abstract picture" without defining it explicitly. The interpretation of this term would be – what the major recognise as different from some random mixture image.
I was working with wide scale of procedural texture generation techniques that were suitable for simulating natural phenomena. After a time, there was a question: is it possible to implement an algorithm yielding the nice abstract pictures including some that might be created by those well-known techniques? It means, to create a "black-box" with nothing on input and a surprising image on output. I was searching for a platform and limitations on the texture space, where I would be able to do that. So the question stays: is there any algorithm that can yield relevant subset of nice abstract pictures?
1.1 Procedural techniques outline
There are many techniques for creating an amazing color patterns. I will briefly mention main ones, which I supposed, are most famous. Examples in form of the images I got after experimenting with them follow.
Explicit functions were used already with first textures in 1974. They are still most frequent, because of their simplicity. Even a chessboard pattern is explicit function. In 1977, Mandelbrot published his first book on fractals. They are so popular that people often tend to link the term procedural texture with fractals. Wide scale of nice abstract pictures can be done using noises and turbulences. Ken Perlin examined first noise in 1985. It can be sad that noise is what brings the irregularity into textures. In nineties ([5], [6]), there was a boom of reaction-diffusion textures. They were invented to simulate natural phenomena like mammalian coat patterns. Many other techniques were developed, up to now.












1.2 Procedural texture languages
In eighties most of texture developers had to work with common programming languages to make a required effect. They were too general for graphical purposes. Source code written to display even a simple pattern might be hundredths lines long. Big effort was taken into building suitable libraries helping to shorten design time. Pixar then came with its RenderMan Shading Language [3], which is still perhaps the most popular tool for writing complex patterns. It is based on the C language syntax and it is strongly influenced by its usage in the robust render system. It got rid of unnecessary implementation details. Writing shader (texture computation procedure) for RenderMan is easy and therefore accessible for many people.
Darwyn Peachey in [2] deals with explicit functions to reach interesting results. He introduced the base stones (simple well-defined functions) and combining technique (layering or composition) - something that he calls "functional toolkit". Peachey writes shaders in RenderMan, but his ideas are portable to any other platform, because textures he got are described in the language of mathematics.
Kurt Fleisher in [8] brought an idea of texture elements called cells interacting with each other. There is a program associated to the cell, which controls its behaviour. Cells are distributed in the space carrying their own information (state variables). They are able to move and to change their inner states. After an evolution of whole system, resulting pattern can be seen. Some older procedural techniques could be simulated this way. Nevertheless, Fleisher uses just first order differential equations as the cell programs, which I think is not sufficient.
Previous accesses were suitable for those deeply interested in the procedural texture generation techniques. Now, many other people want to try making nice abstract pictures. Applications marked as texture creators are now available for anyone. But each one is focusing only on some popular procedural techniques and their possibilities are very limited. Somewhere between commercial applications and theoretic access we can found Darktree Textures software. Main idea of this application is to let the user play with "black-boxes" and to link them together. Each black-box represents a function or an operation and could be parameterised. Result may be passed to another black-box as input. Program offers rich variety of black-boxes.
2. Evolutional Textures
As the term evolutional texture I define the pattern that is a result of evolutional process in the system consisting of the texture domain, initial state and developmental rules. I will not go deeper into definitions. Shortly, texture domain is the space where texture shall be processed, it may be some regular grid or any arbitrary mesh built from the elements, which carry texture information. Initial state is the evolutional trigger. It fills the texture domain with initial values. Developmental rules are responsible for system behavior. Evolution itself is a process that begins at initial time (when initial state is set) and continues in discrete time steps by applicating the developmental rules.
2.1 Reaction-Diffusion Textures
Alan Turing introduced reaction-diffusion textures in 1952 as a model for morphogenesis. They were reinvented in eighties and primarily used for simulating the mammalian coat patterns [4]. Reaction-diffusion technique is an example of evolutional approach.
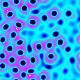
It is based on interaction of chemicals – called morphogens – over the space. Turing described reaction-diffusion by continuous equations. Now, they are used in discrete domain: space consists of discrete cells and the system evolution is performed in discrete time steps. Concentrations of morphogens in the cells are displayed. Depending on particular equations they form arrangements of spots, stripes, spirals, leopard patterns, sand, zebra haunch, etc. Even changing one parameter can change pattern properties. Figure 4 shows four samples from my work.
Computing of morphogen concentration in one cell is done in two phases in each time step. At first, morphogen reacts with other morphogens in the cell. Next, morphogen diffuses from the cell. That means, if conditions allow, its parts are distributed into neighbouring cells. This way the interaction between cells is ensured. Nowadays, the real-time computation and animation of evolution process is possible.
2.2 Practical design
I choose the evolutional textures as a fundament because they can simulate all known texture generation techniques (each algorithm runs in discrete time). But how can one find any common feature for so various techniques? My ambition is to randomly generate developmental rules. Therefore, I have to choose a suitable subset of them by defining their domain, initial state and rules.
Computer graphicians write the programs displaying their results in a raster. I will consider the regular grid derived from rectangular raster because of its simple topology. Basic grid element is called cell. It has a small number of variables determining its state. I use developmental rules in form of the programs associated to the cells. Cell program operates with its variables (it can change their values) and reads also variables of other cells. Each cell has assigned the same program for simplicity. That means, cells differ only in their position and initial state. And finally, I allow the cell programs to access only the variables of neighbouring cells (except of their own).
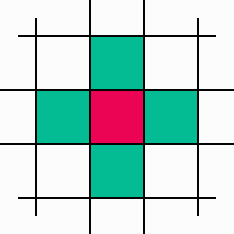
Wide range of implementations may be constructed following these restrictions. What should be noticed is that I will create only 2-dimensional textures. The best texture domain "shape" for me is a torus. It is simply a rectangular lattice of size m´ n, where each cell position is given by integer coordinates [i,j] (0Ł i<m, 0Ł j<n). In addition, it has edges "glued" together, i.e. cells from the top row are adjacent to bottom row cells and cells from the right edge are adjacent to left edge cells. Hence, left neighbour of the cell with coordinates [i,j] is the cell with coordinates [(i+m-1) mod m, j], right neighbour has coordinates [(i+1) mod m, j], upper one [i, (j+n-1) mod n], lower [i, (j+1) mod n], etc. Advantage of the torus grid is homogenity - it has no edges and therefore a seamless texture can be easily made on it.
3 Binary Textures
I was seeking for evolutional texture class in which I would be able to generate developmental rules stochastically. Most simple seems to be binary texture category defined on the torus grid. Suppose the cell has only one binary variable (0/1). Let it allow to communicate with 4 neighbours: on the left, right, upper and lower side. Cell can read theirs variables.
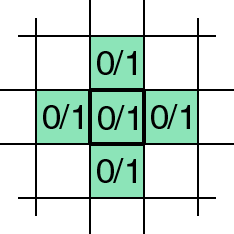
Binary evolutional system consists of m´ n cells with one program associated. This program is evoked mn times in one time step to recompute state of each cell. Its input is the cell variable and the cell neighbours variables, output is the cell variable new value. Program is then a binary function defined on five variables, schematically (left, right, upper, lower, vari) ® vari+1. That means, 25 bits - its output vector, may represent it.
Someone would wonder, what is possible to get with so small program set. Omitting the initial states, they describe 232 = 65536 patterns. Having 32 bits we are able to make for example simple binary reaction-diffusion textures, patterns like chessboard, stripe formations or picture of artificial seashore. It is not very difficult to prove these states. Assigning random binary value at init state is sufficient to bring irregularity to the system.
Suppose having that random init state. Then, any arbitrary 32-bit vector represents a texture (statistically similar textures). In the other words, I found the way to stochastically generate developmental rule of binary texture – random setting of 32 bits. Only a part of 32-bit vectors represents nice abstract pictures, major part is a trash. How often does the nice abstract picture programs occur in the sequence of randomly generated programs? I made an application for finding an answer. It sets the system init state and 32-bit program (developmental rule) stochastically and then makes an evolution, displaying it on the screen. User can stop the evolution, see its result and go to another attempt.
I did not expect any success. But after only a few minutes of experimenting with ready program I saw many interesting binary patterns – patterns that are not just random mixture binary arrangements.

I was surprised: almost one from five texture might be marked as a nice abstract picture. I saw the familiar-looking patterns and also amazing formations I have never seen before. If I wanted to compare the situation with explicit binary pictures (it is not exactly correct): how great are my chances to see any interesting thing in the straightforward random generated binary picture?
What about making nice abstract binary picture without user interactivity? I started to study binary textures behaviour and focused on their convergence. I noticed that each convergent system forms an interesting pattern. There were also binary systems that evoluted into interesting image and then began to repeat part of their "life-cycle", e.g. the system could be stable but there were independent cells switching variable values to opposite than in the previous step. These systems are stable in fact – they fulfil "weak condition of stability": system is stable if its state history is finite state sequence repetition. In computer science a "strong condition of stability" is preferred: system is stable if its history is one state repetition (we will use this definition). System converges if it becomes stable and diverges in all other cases. Binary evolutional texture system convergence depends on the mesh shape and initial state.
I developed an algorithm determining binary evolutional texture system convergence without considering init state. On input, there is a 32-bit program (developmental rule) and a mesh. Algorithm is seeking for the stable state of evolutional system represented by this program. This is done by reverse pattern (states) completing – in each step one cell and its four neighbours are examined to fit in the pattern.

Rather than describe the algorithm formally I will discuss example of one step. Suppose that algorithm led to the situation on the Figure 10. There are cells with preset state (0 or 1) and the white cells – they haven’t set their state, yet. Algorithm wants to examine cells bounded by thick lines. It will search trough the 32-bit boolean function (program given on input) to find suitable assignment of arguments to the function value. It must have the form (left, right, upper, lower, var) ® var, in general (stability condition). In our case: (1, ?, 1, ?, 0) ® 0. Question-marks are substituted by binary values. If no substitution equal to function assignment is found algorithm knows the system configured as Figure 10 shows is not stable. If such substitution is found algorithm should set cell states marked by "?" to appropriate values. Together with presets the new two cells form a stable arrangement.
Algorithm makes recursive steps. If it reaches the unstable situation it will go one step back and tries another substitution. It succeeds, if whole mesh is filled by cells with set values. This situation is shown on output. It is the init state and it will never change after an evolution. Algorithm knows there is no stable arrangement after trying all possible situations without mesh fulfilment. I use an optimalization not to waste lot of time in the phase of choosing the place where new step will be done: smaller the number of unexplored cells (marked by "?" in the example) in the neighbourhood is, smaller the effort to find suitable substitution in one step is needed. However, algorithm complexity is very high (because of backtracking). I developed a simple application using convergence-determination algorithm for PC capable of running in DOS mode. User can define size of rectangular grid, computer generates random developmental program and determines its convergence. If it doesn’t converge (no initial state leads to stable state), user is announced. If it converges, the result (initial state) is displayed. Application runs fast (taking the time from fraction of second to one minute on the Pentium III 450 MHz processor) only working with up to approximately 50 cells in the square.
Using algorithm mentioned above there is no problem to create a texture generator yielding various nice abstract pictures in the binary domain: 32-bit programs are randomly generated unless one that converges on the given mesh is found and system’s stable init state is obtained. Disadvantage of this approach is the limitation I use for binary evolution textures: only one cell variable is used and only four cell neighbours are taken into consideration. Increasing these numbers makes computation of evolution very slow.
4 Language for Evolutional Textures
We can combine pixels from a binary texture to reach more than 2 colors. Wider color scale is needed for patterns resembling originals in nature. Therefore we must extend binary evolutional textures to more complex model. First, a cell variable should be real number. Next, there ought to be more than one variable in the cell. Moreover, variables may be formed into structures. Memory space may be associated to the cell. Also number of neighbors cell can access could be increased. Torus grid may be upgraded to any other mesh structure (even more than two-dimensional).
In general, we can think about the cell like about node encapsulating memory space and a distributed program. It cooperates with other nodes in the net by message communication. This platform is robust enough to write program making any reasonable texture, but it is hard to manage; program coding would take lot of time, evolution on distributed system would be slow, it is uselessly complex. Let’s go back to simpler platform. Developmental rule can be viewed as an assignment f (x1,x2,...,xn) = (x1,x2,...,xm), where m is number of cell variables (memory size) and n is number of all variables that cell is able to read including its own (mŁ n). Splitting it into m functions we have f i(x1,x2,...,xn) = xi, 1Ł iŁ m, where f i is rule for variable xi. How can be this rule described? There are two accesses. First is based on functional composition: f i(x1,x2,...,xn) = f1(x1,x2,...,xn)· f2(x1,x2,...,xn). It is suitable in some cases, e.g. Kurt Fleischer [8] uses first order linear equations as the rules. Nevertheless, it is hard to write – and also read – more complex rule in that way. Therefore I prefer writing the rules in conditional form: f i(x1,x2,...,xn) = if bool(x1,x2,...,xn) then exp1(x1,x2,...,xn) else exp2(x1,x2,...,xn).
Texture language
There is one important thing about extending binary textures: I don’t know, how to stochastically generate developmental rules for them. Imagine a cell only with one real-number variable. It is impossible for user to list down all cell states and assign a value to each one as it was in binary textures. I was trying to create a simple language in which developmental rules could be written. Simple in the way that one could easily write a "program" (developmental rule) using it, the program could be quickly interpreted (fast evolution) and maybe random program generator can be found for the language. I developed one and call it Texture Language.
I am still using torus grid as a structure for texture domain. In Texture Language cell consist of linear array of real-number variables. I found out that 6 variables are enough for creating large amount of familiar patterns. There is a possibility to allocate up to 9 variables. They are accessed by index numbers. Program in the Texture Language consists of rules: one for each variable. Rules are identified by header in their beginnings: after token [i] rule for variable i is expected. Each rule is a conditional. It has true and false branches, which may be again conditionals or ready values. To gain faster interpretation there is one difference to common conditional semantics in Texture Language. In the evaluation phase, as interpreter goes along the true/false branches with regard to conditions, it never returns back, even after no value is assigned to the particular variable at the branch end. Cell is able to access 8 neighbours: upper left, upper right, lower left and lower right adjacent cells were added into neighbourhood. Neighbour cell variables can be read using tokens left[i], right[i], upper[i], lower[i], ul[i] (upper left neighbour), ur[i], ll[i], lr[i], where i is variable index number.
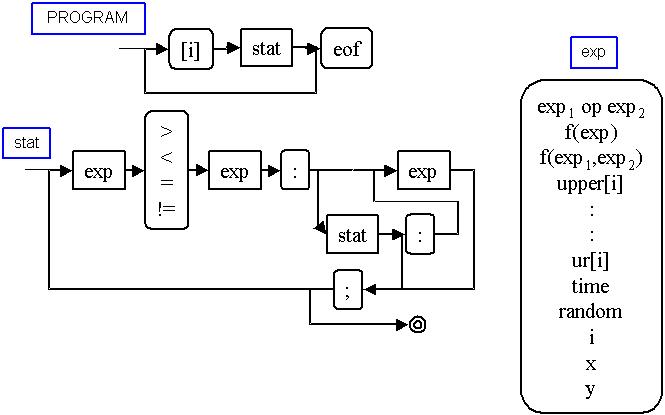
I have developed the Texture Language interpreter application running as MS-DOS real mode executable capable of showing the results in VGA graphics. It expects Texture Language file name on the input (command line). Program should be 8-bit ASCII text file with .tla extension. Text lines and words that are not recognised as the parts of rules are supposed to be user remarks. If the application doesn’t know how to interpret the program, it reports error message according to situation and exits. Otherwise, evolution is triggered. There is no initial state preset (program should do that), evolution begins by time 1. Results are displayed in form of layers – each layer is a rectangle showing the state of all variables with same index (one pixel per one cell). I use 64-degree white-to-black palette where black color represents minimal actual value from the layer and white represents the maximal one.

In figure 12 there is a program making an "average noise". It fills only the first layer of evolutional system. Rule for variable 1 sets it a random value (between 0 and 1) while time<3. Up to time 40 a process of averaging neighbouring variables begins: values from left and up neighbours and from the cell itself (center[1]) are averaged and the result is stored into variable 1. It causes an effect of smoothing a random pattern while it slightly rolls in the lower-right direction. All described work can be done by writing four lines! No initialisation, no care of the output. User may concentrate on the algorithm’s core in phase of coding it into the Texture Language.
Not all texture generation techniques are so easily transferable, of course. Texture Language is most suitable for implicit raster techniques. What are its possibilities? Formally: how large is a texture set it describes, and which texture classes it includes? It is clear that binary textures belong there. Because of similar nature, it is possible to simulate simple cellular automata by Texture Language. Kurt Fleischer’s cellular programs can be written in it. As it was shown, many noise descendants are easy to write. Texture Language is very suitable for reaction-diffusion technique – algorithms may be straightforward transcript from the equations.



Texture Language is designed for texture developers, that means one must know the technique (at least have its formulas) before coding it. In addition, the sense of distributed systems is required. Some features are specific for the latticed-based nets. It is mainly the metrics (routing, traversing and other similar problems). It is very easy to examine how is the communication between cells performed. For example, broadcasting the message from the plane centre to other cells. Influence of Manhattan metrics can be found. You can use the Euclidean, of course. Each cell can access its coordinates (x, y symbols) and real-number arithmetic is also supported (e.g. sqrt, sin, cos). Expressions are written like in ANSI C standard, nested brackets can be used. Therefore, also explicit function visualisation may be written.


5 Conclusions
Many textures may be produced using evolutional systems. On the other side, there are lot of textures developed by certain techniques, that are much more faster. Geometry-based textures (e.g. fractal snowflake) are hard to describe by an evolution: even there is no problem to code incremental line-drawing algorithm in that way, processing this in the Texture Language is wasting of its power. Figure 16 is an example of unnefective texture Language appplication. Algorithms of explicit nature can be simulated, but this is not what Texture Language was developed for. I focused on the techniques generating textures on some mesh, because they are able to handle complex patterns occurring in our nature. I used only plain grid with regular topology, but the mesh can be directly created on the object’s surface – cat coat with its irregularities can be accomplished in this way.
Now, we are ready to answer the question from the beggining (is there any algorithm that can yield relevant subset of nice abstract pictures?). If the binary domain is satisfying, we are able to construct generic texture algorithm. Not all binary textures can be found on its output, but the technique described in this paper subsumes many of them. Problem of defining "nice abstract pictures" may be solved on the idea that all patterns generic texture algorithm gives are nice abstract textures. If a powerful generic texture algorithm would be constructed, we can say also that no other pattern is nice abstract picture. However, we cannot really define what is and what is not nice.
Texture Language, I developed, is little bit a helper for texture developers. It has some drawbacks, of course (one of them is that program cannot change the grid size – program initialisation section shall be supported later). I don’t want to compare it with shader languages, because its origin is somewhere else. It is a language, which "programs" I thought, could be generated stochastically. If someone is able to ensure random program generation in this way, let me know, please.
6 References
[1] J. Žára, B. Beneš, P. Felkel: Moderní počítačová grafika, Computer Press, Prague, 1998.
[2] D. S. Ebert, F. K. Musgrave, D. Peachey, K. Perlin, S. Worley: Texturing and Modeling: A Procedural Approach, Academic Press, Cambridge, 1994.
[3] T. Porter: Writing Surface Shaders, in T. Apodaca, L. Gritz, course chairs: Advanced RenderMan: Beyond the Companion (SIGGRAPH’98 Course 11), pp. 30-50, 1998.
[4] M. Walter, A. Furnier, M. Reimers: Clonal Mosaic Model for the Synthesis of Mammalian Coat Patterns, Proceedings of Graphics Interface’98 – Vancouver, 1998
[5] G. Turk: Generating Textures on Arbitrary Surfaces Using Reaction-Diffusion, in W. Sedeberg, editor: Computer Graphics (SIGGRAPH’91 Proceedings), volume 25, pp. 289-298, 1991.
[6] A. Witkin, M. Kass: Reaction-Diffusion Textures, in W. Sedeberg, editor: Computer Graphics (SIGGRAPH’91 Proceedings), volume 25, pp. 299-308, 1991.
[7] B. Zitová: Textury a jejich výpočet reakční difuzí, diploma work, Matematicko-Fyzikální Fakulta Univerzity Karlovy, Prague, 1995.
[8] K. W. Fleischer, D. H. Laidlaw, B. L. Currin, A. H. Barr: Cellular Texture Generation, SIGGRAPH’95 Proceedings, ACM SIGGRAPH, 1995.
[9] B. Mandelbrot: The Fractal Geometry of Nature, W. H. Freeman, San Francisco, 1982.