Collision detection between moving objects using uniform space subdivision
Smiljan Šinjur
smiljan.sinjur@uni-mb.si
Laboratory for
Geometric Modeling and Multimedia Algorithms
Institute of Computer
Science
Faculty of Electrical
Engineering and Computer Science
University of Maribor
Maribor / Slovenia
Contents:
1. Introduction
2. Interaction between VRML and Java in computer simulations
3. Triangulation
4. Collision detection
4.1 Raw method
4.2 Space subdivision method
5. Triangle-triangle intersection
6. Conclusions
Fast and accurate collision detection between general solid models is a fundamental problem in solid modeling, robotics, animation and computer-simulated environments. The most of the algorithms are restricted to an approximate collision detection. In the paper, we also present an algorithm for collision detection between 3D objects. The algorithm can be used in simulation robotics or any other simulation in 3D space. It works only with triangles, so the objects must be triangulated first, and obtained triangles are tested for collision detection then. Two methods are described for a triangle intersection test. The first one is a raw method, which tests all pairs of triangles in the space. Besides it, the improved algorithm with the space subdivision is given. The raw method is slow and it is not suitable for real time simulation. The space subdivision method is faster and it is expected to be quick enough for many real time simulations. The simulation is modelled and visualised in VRML, and the collision test and movement controlling are implemented in Java.
Keywords: algorithms, collision detection, space subdivision, triangle-triangle intersection, geometry.
In recent years, the use of robot systems has rapidly increased, but these systems are still very expensive. Therefore, they must be protected from any damage. Unfortunately, it is usually impossible to directly prevent collisions between robots and objects surrounding them, while a robot cannot see its surroundings. A danger of going something wrong with a real physical robot is large. A small inattention when moving a robot can cause incorrigible damage or high expenses of repair. A robot could be equipped with “eyes” in a form of sensors and precise measuring instruments, but this would increase cost significantly. Therefore, it is much cheaper to use computer simulated robots [1], [2], specially for teaching purposes in robotics. Of course, it is expected that a collision detection is included in a simulation as well [3], [4]. It prevents collisions between a robot model and models of other objects. By reporting an error of collision in simulation, a damage that could be made on a real robot performing the same action as its model is prevented. But the simulation with collision detection is not usable only for students learning about robotics. Information obtained from the simulation can also be used to contol a real robot. A computer model represents a real robot in a virtual world, which is a precise copy of robot's surroundings. The robot may repeat moves, which were previously recognized safe by simulating them on robot's model, and of course, the robot should not perform an operation, if its model collided with some virtual object during simulation.
The previously mentioned papers [1], [2] describe controlling a physical robot with a computer via internet. In this paper, we give a description how the collision detection is performed in simulation. This simulation is programmed with VRML and Java. The Virtual reality modelling language (VRML) is a multi platform file interchange format for building 3D graphical models. The VRML standard defines semantics found in 3D modelling applications e.g. construction of geometric primitives, hierarchical transformations, lighting sources, viewpoints, animation, etc. Java is also a platform independent programming language, which can interact with VRML scenes. In VRML, we create a virtual robot and the world that surrounds this robot, and the robot movement is controlled with Java components.
The paper is organised into six chapters. After this introduction, a problem refered in the continuation is briefly discussed and the main actions are listed. In the third chapter, triangulation of particular VRML shape nodes is described. Namelly, our collision detection operates with triangles only, and therefore, more compex shapes have to be triangulated first. After this, two approaches to collision detection are explained: the raw method and the space subdivision method. In the fifth chapter, mathematical background of a triangle – triangle intersection test, which presents the fundamental operation of the collision test, is observed. Finally, our work is briefly highlighted once more in the conclusion, and our future work in this field is described.
2. Interaction between VRML and Java in computer simulations
For controlling a real robot by help of a computer, it suffices to calculate whether the robot collides with some other object, but really efficient simulation should use all abilities of computer graphics to visualize a model of the robot and its virtual surroundings. We have used a possibilities offered by VRML to implement this task. The VRML is very suitable for simulations in 3D environment, because a user only has to describe the geometry and the lighting parameters of the virtual world, and all the rest is done by the VRML browser. The user need not think how to implement projections, rendering and navigation in a virtual world, while all these tasks are provided by the browser already. Besides this, the VRML browsers are typically designed as additional components to standard internet browsers, and therefore, VRML brings virtual worlds to internet.
The main building element in the VRML language is called a node. It unites a set of fields, which can present parameters of types known from other programming languages, or other (nested) nodes. In VRML, the geometry is described with so-called shape nodes like a Sphere or a Cone. There are two possibilities. The first one is to use predefined primitive shapes. These shapes are boxes, cones, cylinders and spheres, which can ber represented by the Box, the Cone, the Cylinder and the Sphere nodes. Beside to the primitive shapes, the IndexedFaceSet node can be used to represent a 3D object. By this node, the face geometry is described. Among all, the IndexedFaceSet node contains the coord field, which specifies the coordinates of points available for building faces within the face set. A complex object can be represented by a group of primitive types, or by a set of faces described by the IndexedFaceSet node, or by a combination of all these nodes.

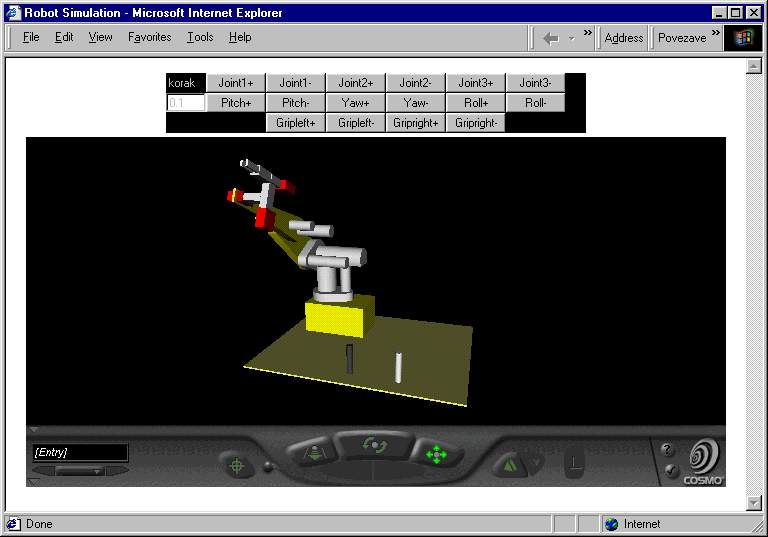
Figure 1: A robot arm created in VRML and controled with Java buttons
In Figure 1, an example of a virtual robot is shown. The virtual world is built from different shapes (Box, Cone, Sphere, Cylinder and IndexedFaceSet). A single shape or more shapes build objects. Interesting objects presenting the parts of the robot are named joint1, joint2, joint3, pitch, yaw, roll and gripper. The static table and two cylinders lying on it are also objects. At first, we have to gather a geometry of all shapes to be able to build geometry of all objects.
Besides nodes and fields, the third consistent part of the VRML language are events. Events bring dynamics into VRML world. We use them to change coordinates of particular objects. Actually, each object is nested, one by one, in so-called Transform node, and the values of fields of these nodes, which represent parameters of geometric transformations (rotations, scalling and translation), are modified. A user can interactively modify these parameters by using Java buttons at the top of the window (see Figure 1). In this way, movement of the robot is controlled. A part of the robot may be moved only if it would not collide some other object (the table, two cylinders on the table or other part of the robot) in its new position. The collision detection is also implemented in Java. The shapes are exported from VRML into the Java application first. While the collision detection is performed on triangles only, the objects being moved have to be triangulated then. After the triangulation, triangles are tested for intersections. If some intersection is determined, the application reports error, otherwise transformation parameters for objects being moved are exported back to VRML (they are routed to appropriate fields in appopriate Transform nodes), and the VRML browser can visualize modified virtual world. From Figure 1, it can be noticed that we use the browser Cosmo Player.
Structure of the whole system and interaction of all included parts are shown in Figure 2.
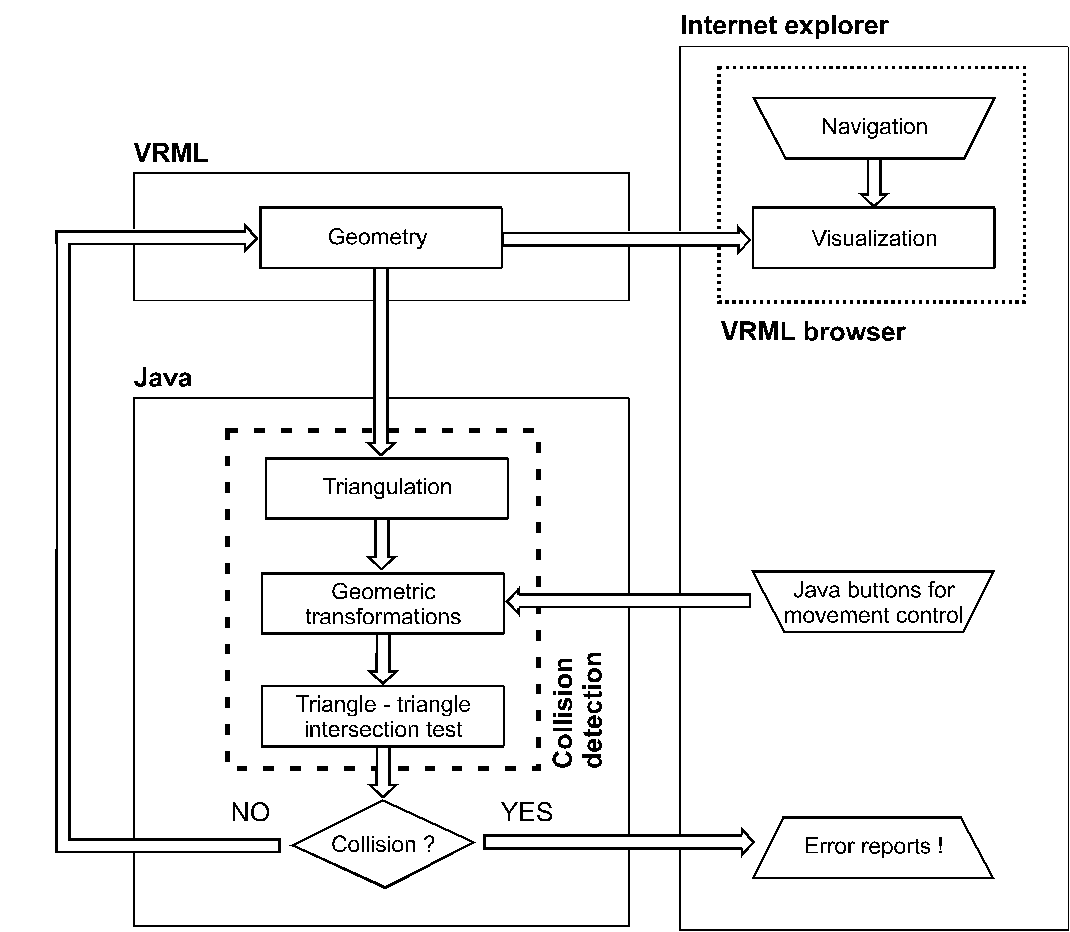
Figure 2: The collision detection system based on interaction of VRML and Java
Our collision detection, as mentioned before, is performed on triangles only. Therefore it is necessary to triangulate every shape. Each shape is decomposed into several triangles. A triangle is described by three points (vertices): Triangle(P0, P1, P2).
The primitive shapes are triangulated in the following way:
a)  b)
b) 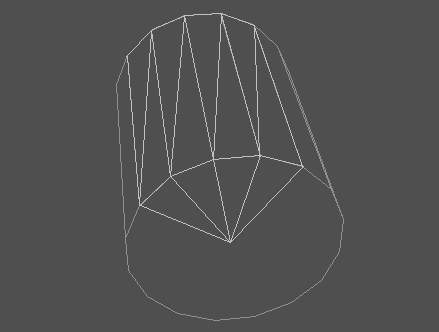
c) 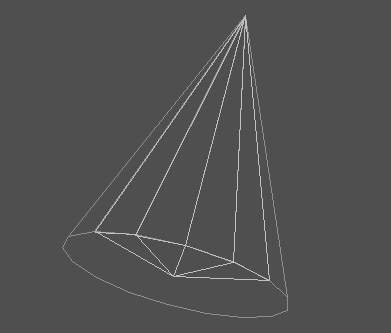 d)
d) 
Figure 3 : Trianglulation of a) Box, b) Cylinder, c) Cone, d) Sphere
Non-primitive shapes represented by IndexedFaceSet are triangulated in the following way. When building shapes with this node, it must be considered first whether the shape is convex or concave. All the shapes mentioned before are convex. At the curent level of implementation, our application also allows only objects with all the faces described by the IndexedFaceSet node being convex. Typically, the coord field includes the Coordinate node. The coordIndex field specifies a list of the coordinate indices refering to the points describing a single face or more faces. The points are specified in the coord field. The convex field is TRUE or FALSE indicating whether all the faces in the face set are convex. The IndexedFaceSet node has also some other fields, but they are not so important for representing geometry. More imformation on VRML nodes and the structure of VRML files can be found in the book [6].
From IndexedFaceSet, we obtain several planar polygons. The polygons can vary in number of vertices. Each polygon must be triangulated. From a polygon with n vertices {P0, P1, P2,…, Pi, Pi+1,…, Pn}, we obtain n-2 triangles sharing common top vertex: (P0, P1, P2), …, (P0, Pi, Pi+1), …, (P0, Pn-1, Pn). In figure 4, an example of a pentagon is given. After triangulation, we obtain three triangles.
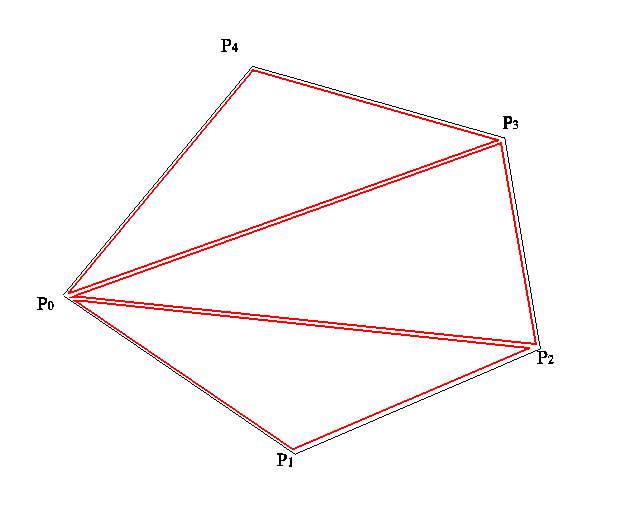
Figure 4: Triangulation of a pentagon
With these nodes (Box, Cone, Cylinder, Sphere and IndexedFaceSet), we can describe any robot in space. Later, more complex concave faces will also be available in simulation, but for simple use for educational purposes the described shapes are sufficient.
Every object is described with a list of triangles. Therefore, every triangle has an id, to tell us to which object the triangle belongs. To every triangle, a 4x4 matrix belongs also. This matrix describes the position of the triangle in space. When transforming- translating, scaling or rotating an object – a triangle that presents the object, we change the values in this matrix, not the vertex coordinates of triangle. Real position of the triangle in space is then obtained by multipling all the vertices of the triangle by the matrix.
Every object – each triangle that represents the object, also has a tag, which describes, whether the object is static or dynamic. If the triangle has a static tag, it means that it cannot be moved. For example, the table in Figure 1 is a static object. Dynamic triangles can be moved.
Each triangle in our virtual world has its own id, which identifies the object that the triangle is a part of. A triangle is also equipped with the matrix, which describes its position in the space. When some objects are being moved, the matrices of all triangles that represent these objects must be corrected. Collision detection is then performed on these triangles. Two triangles need not be tested if :
Therefore, the triangle-triangle intersection test is made only when we compare two dynamic triangles or a static and a dynamic triangle. Before calling a routine for triangle-triangle intersection test, all triangles must be described with points at correct positions. All three points of both triangles must be multiplied with the transformation matrix of the corresponding triangle.
In the next two subsections, we describe two methods for collision detection. They differ significantly in number of triangles that have to be tested. First, the raw method is described. This method is slow and it is not suitable for a real time simulation. The second method is based on space subdivision. It is expected to be faster than the raw method for more than 80 %.
This is the simplest method for testing collision detection. Each triangle is tested for intersection with all the others triangles in space. When testing a pair of triangles, both triangles must present parts of two different objects. There are two possibilities when to stop the intersection test :
In robot simulation, it is usually expected that the object collision rarely appears. Every user avoids these situations. The most collision process time is needed when there are no collided objects in the space. For this situation, the O(n2) time complexity is obtained, where n is the number of triangles in the space. Actually, the number of intersection tests is a bit lower while we do not test pairs of triangles gelonging to the same object, but it is in general still O(n2).
If we have a lot of triangles in the space, time spent for testing collisions is very long. For example, if there are two thousand triangles, the triangle-triangle intersection is made up to two millions times (probably less, while we do not test triangles of the same object). The robot in Figure 1 is described with approximately 1500 triangles, and requires about a million of repetitions of the intersection test. Beside to this, the intersection test is not a simple operation. For faster and real time simulations, some acceleration technique is recommended. In the next subsection, we propose one of them – the space subdivision method.
Here, we employ a 3D generalization of the acceleration technique, which is widely used in applications of computational geometry, especially in GIS, where we have to deal with large amounts of geometric data. We divide the space into subspaces usually named cells and then determine for each geometric element (a triangle in our case) the cells that at least partially contain the object. After this, it suffices to test for intersections only the elements belonging to the same cell.
It is important to divide the space efficiently. It is recommendable that the cells are simple shapes to accelerate the containment test whether an element belongs to the cell. The most natural way is to use rectangles in 2D, and cubes in 3D space, both with the sides parallel to coordinate axes. Beside to this, it is desired that a particular cell does not contain to many geometric elements. Note that a particular element can spread over more adjacent cells. We use a heuristics to determine size of the cells. We use an average length of all triangles in all three coordinate directions. Dimensions of a cell are then calculated as follows.
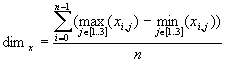
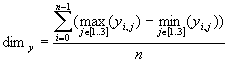
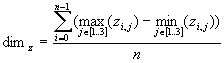
It is expected that a particular triangle spreads over a small number of cells, and that each cell contains a small number of triangles. Consecutively, the number of repetitions of the triangle-triangle intersection test is also small. The time complexity for this method is O(a m2), where a is the number of cells, and m is the avarage number of triangles in a particual cell. The value of m is always much smaller than the number of all triangles in the space (m << n).
The space subdivision is performed only once at the begining of the simulation. The space has to be limited in a way to assure that none of the objects would fall out of it later after performing geometric transformations on objects. This seems impossible, but we should not forget that we usually know the real-world environment of the robot being simulated (the robot is placed in the room, for example).
Each cell has a list of triangles that are at least partially contained in the cell. If the transformation is performed on an object, it must be performed on all triangles that form this object. Such triangle must then be removed from all cells containing it before the transformation, and inserted in the triangle lists of cells containing the triangle after the triangulation. After this, a triangle-triangle intersection test for all pairs of triangles in particular cells is performed. To increase efficiency, any two triangles of the same object and any two static triangles are not being tested.
This method is in general much faster than the raw method. If we have two thousand triangles, and assume that we divide the space into one hundred twenty-five cells (five subdivisions in each coordinate direction), we obtain sixteen triangles per cell in average. The number of triangle-triangle intersection tests will then be about thirty thousand (152 * 162) or even less. This number is much smaller than two millions obtained with raw method.
In Figure 5, an example of space subdivision is shown. We use a 2D example, while it is much easier to draw it, but the situation in 3D space is analogous. We have four triangles A, B, C and D belonging to four different objects. A lies in the cells [0, 0], [0, 1], [1, 0], [1, 1], [2, 0] and [2, 1], where the first number in the coordinate pair represents the position of a cell in x-direction, and the second one in y-direction. B is placed in the cells [2, 0], [2, 1], [3, 0], [3, 1] and [4, 1]. C spreads over the cells [0, 1], [0, 2], [1, 1], [1, 2] and [1, 3], and D is positioned into the cells [2, 3], [3, 2], [3, 3], [3, 4], [4, 3] and [4, 4]. We only have to test the pair [A, C], which both occupy the cells [0, 1] and [1, 1], and the pair [A, B], while both the triangles are partially in the cell [2, 1]. With the first pair, an intersection is determined, and with the second one, it is not. Note that the triangles A and C need not be tested in the cell [1, 1] once more, after they had been tested in the cell [0, 1] already.
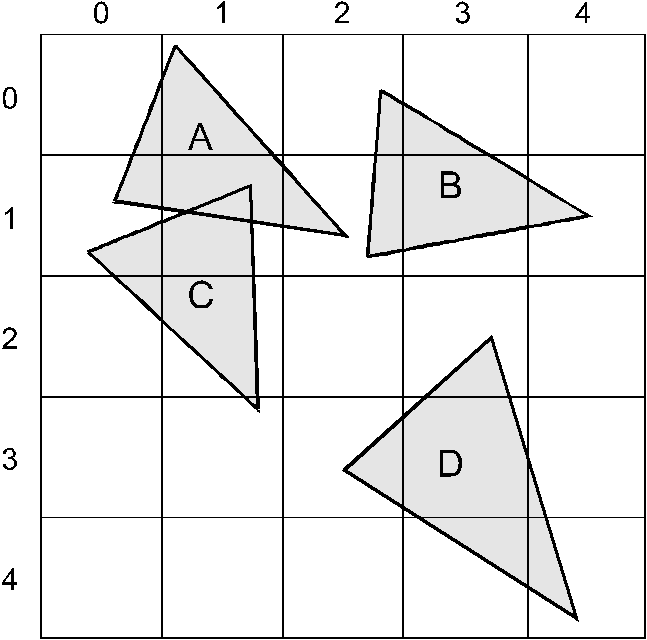
Figure 5: An example of space subdivision from 2D space
5. Triangle-triangle intersection
No matter whether we use the raw method or the space subdivision method for the collision detection, the triangle-triangle intersection test is performed in the same way. This is the basic operation of our collision detection algorithm and its is executed really often, so it is expected to be fast enough. The described test is based on fast elimination of triangles which do not intersect.
Three vertices of each of the triangles define a plane in 3D space. Regarding the mutual position of two triangles and the planes P1 and P2 defined be these two triangles, three different situations are possible.
The paper indroduces the collision detection with space subdivision that can be performed in simulations. The implementation is based on interaction between the VRML and the Java part. VRML is employed for geometry representation and visualisation, and the Java application provides the collision detection and movement control by Java buttons. Objects are triangulated first. When a part of the robot being simulated is tried to be moved, new positions of this part i.e. all the triangles forming it are calculated by performing geometric transformations. After this, the transformed triangles are tested for intersections. The movement is confirm if no intersections are detected, otherwise the collision detection is reported. The number of triangles is typically large and testing all the pairs would require a lot of time. The space subdivision is used to accelerate the algorithm by reducing the number of pairs that have to be tested. The space is subdivided into cells, and only the pairs of triangles, which belong to two different object and at least partially lie in the same cell, have to be tested. Experiments have proved that this method is generally faster than the raw method for approximately 80%.
The described simulation with collision detection is intended to be a part of the bigger project for controlling a real robot via internet. The simulation part will be generalized to handle objects with concave sides as well. Besides this, the whole project will be organised as a client-server application. Users will address the server, and this will communicate to the robot.
I would like to thank to Dr. Riko Šafarič and David Podgorelec, MSc, both from the Faculty of EE & CS of the University of Maribor, for their valuable suggestions to my work.
[1] Šafarič, R., Debevec, M., Parkin, R. M. and Uran, S.: Telerobotics experiments via Internet in IEEE trans. ind. electron., Apr.2001
[2] Šafarič, R., Calkin, D. W., Parkin, R. M. and Czarnecki, C. A: Virtual environment for telerobotics in Integr. comput.-aided eng., Apr. 2001
[3] Hudson T., Lin M., Cohen J., Gottschalk S. and Manocha D.:V-COLLIDE: Accelerated Collision Detection for VRML, in Proc. of VRML, 1997.
[4] Lin M. and Gottschalk S.: Collision Detection between Geometric Models: A Survey, in Proc. of IMA Conference on Mathematics of Surfaces, 1998.
[5] Ponamgi M., Manocha D., and Lin M.: Incremental Algorithms for Collision Detection Between Solid Models, in IEEE Transactions on Visualization and Computer Graphics, 3(1), pp. 51-67, 1997
[6] Ames L. A., Nadeau D.R. and Moreland L. J. : VRML 2.0 Sourcebook, Wiley computer publishing, 1997