Constrained Delaunay Triangulation using Plane Subdivision

This paper presents an algorithm for obtaining a constrained Delaunay triangulation from a given planar graph. The main advantage towards other algorithms is that I use an efficient Žalik's algorithm, using a plane subdivison for obtaining a Delaunay triangulation. It is used for insertion of points into existing triangulation. The other part of algorithm presents a method for inserting edges, already proposed by Anglada. The algorithm is fast and efficient and therefore appropriate for GIS applications.

Keywords: Constrained Delaunay triangulation, two-level subdivision, computational geometry, GIS

Triangulation of set of points on the plane presents a partition of an area, surrounded by a convex hull. Triangles are composed by vertices, given as an input. But if the triangles fulfill additional condition of an empty circumcircle, they present a Delaunay triangulation (DT) [9]. I will go a step further, as many have taken before, by constructing a constrained Delaunay triangulation (CDT). The input is now a planar graph G which consists of vertices V and non-crossing edges E (G = {V, E}). The edges E are actually edges of future triangles, obtained by triangulation.

CDT algorithms can be divided in the same way as DT algorithms, into three main groups:

• Algorithms based on "Divide and conquer" strategy
  As usually, we divide the input set into smaller sets. They can be divided using different approaches, like ribbons or areas. When the sets are small enough, they are trivial to triangulate. The last and the most difficult step is merging two sets together. Those algorithms are quite demanding to implement, however, they are convenient for parallel processing (Hardwick [5] A good example was proposed by Chew [2]. A succesive refinement of the Delaunay triangulation was described by Ruppert [6], where additional Steiner points are used.
• Sweep-Line algorithms
  They use an imaginary sweep-line which divides a working area into two sub-areas. If we watch the area behind the sweep-line, we can see that it has already been triangulated. Yet, the area before it still waits to be processed. Each step adds a new triangle to existing triangulation. This is achieved by connecting a new point or an edge to the boundary of the current triangulation considering the Delaunay criterium. Very popular algorithm was introduced by Fortune [3]. His algorithm was developed to construct a Voronoi diagram [1] - a dual graph of Delaunay triangulation. Shewchuk [7] presented a successful algorithm for constructing higher-dimensional CDT.
• Incremental algorithms
  Are the most popular algorithms today and probably the simplest to implement. They build triangulation gradually, by inserting new vertices or edges. Every step preserves and ensures the rule of empty circumcircle (Guibas, Knuth and Sharir [4], Žalik and Kolingerova [9], Vigo [8]). There are two groups of incremental algorithms:
  • incremental search algorithms,
  • incremental insertion algorithms.

Constrained triangulation was first developed for net formations in the field of finite elements analysis. Today, it is often used in CAD applications and geographic information systems (GIS). An example is triangulation of the terrain which already contains elements that could be represented as edges (roads, rivers, borders). Typical CDT applications include motion planning, collision detection and determination of minimal bounding tree as well. At this point, I have to mention that CDT can not always assure Delaunay criterium, but it can come near. Main reason lies in input constraints, which can violate the criterium.

This article presents an algorithm, which is a combination of two known algorithms (DT algorithm using a nearest-point paradigm, presented by Žalik and Kolingerova [9] and an incremental CDT algorithm explained by Anglada [8]). Sections 2.1 and 2.2 describe each idea in details. At the end, a conclusion, based on results will be given.

---

2. The algorithm

The presented algorithm belongs to a group of incremental insertion algorithms. Its structure consists of two parts:

• insertion of points [9],
• insertion of edges [8].

2.1. Insertion of points

The bottleneck of incremental DT algorithm is the search for a triangle, into which the currently integrating point falls. Žalik and Kolingerova [9] have transformed the problem into finding the closest point, which takes less processing time. Three main steps of the algorithm are:

• Initialization,
• Triangulation,
• Finalisation.

To make our algorithm work fast, the searching structure has to be initialized. The proposed structure is two-level uniform plane sudivision (2LUPS). The plane, which contains all points, is divided into cells (the first level). In case of non-uniformly distributed input points some cells can become overpopulated. Therefore an additional variable Treshold) is defined. When the number of points in cell exceeds Treshold, cells are divided again (the second level). 2LUPS structure is a combination of uniform subdivision (the number of cells equals in both, x and y direction), used for the second level, and adaptive subdivision at the first level, which uses heuristics [9]. The most appropriate cell division in second level forms 16 new cells.

Due to the insertional nature of this algorithm, determination of artificial triangle is to be done first. The triangle has to be constructed large enough, so all points fall inside of it.

Insertion of the first point is handled under initialization. The result is a big triangle, split in three smaller ones. This step is trivial, because triangulation is definitely a DT (Figure 1a).

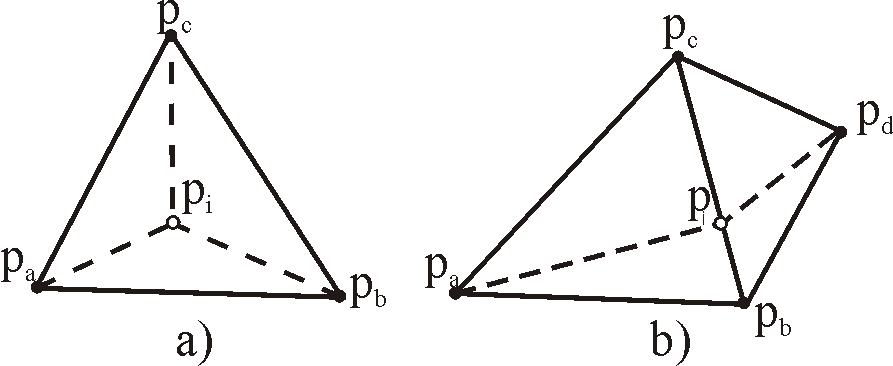
Figure 1: Inserted point p_i splits one triangle and forms three new triangles (a) or splits two and forms four new triangles (b), when it falls on the common edge.

Triangulation is the main process. It consists of two steps. The first step is finding a triangle containing inserted point. This step uses a 2LUPS searching structure and a searching mechanism, usually performed by so-called spiral algorithm, which is used here[9]. First, the point is inserted into a cell of 2LUPS structure. Then, a search for the closest vertex is started (Figure 2). Here, we can see the idea presented by \v Zalik and Kolingerova [9].

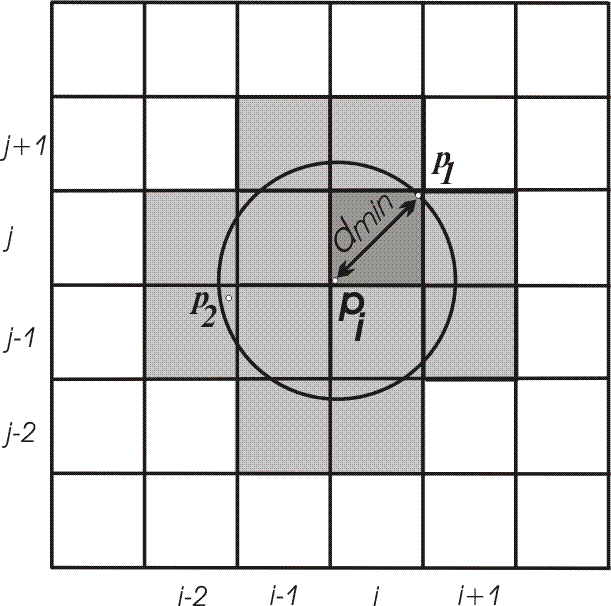
Figure 2: Finding the closest point.

In Figure 2, inserted point is p_i. A distance calculate a distance d_min to the closest vertex in this cell (p₁) is calculated. Shaded cells are being searched (they could contain a vertex within a circle, centered in p_i with radius d_min). When vertex p₂ is located, d_min is updated and the search continues in cells intersected by a new circle (now defined by a new radius d_min). There are no other vertices in the cells, so the closest is p₂}.

After the closest vertex is found, it is possible, that it belongs to one of the triangles containing the inserted point. If not, the next closest vertex has to be found. This is easy, because the candidates are previously examined vertices.

The second step is splitting the corresponding triangle into three or four sub-triangles (Figure 1a and Figure 1b), which are then checked for empty circumcircle criterium (Figure 3). If a triangle fails the checking, it must be legalized. This means that a common edge of the tested triangle and its edge-neighbour must be flipped to obtain two new triangles. Again, they must be tested. The procedure is implemented recursively.

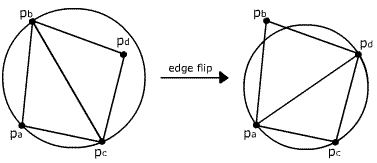
Figure 3: Triangle fails Delaunay criterium and edge flip must be done.

The final step is finalization. Its basic task is a removal of triangles containing the vertices of artificial triangle, formed in initialization. The algorithm works with time complexity of O(n^1,1) for most cases. The worst time complexity is O(n²), where n is number of inserted points.

2.2. Insertion of edges

The currently inserting edge is defined by vertices that are already a part of triangulation. Figure 4 shows an example of the whole process of edge insertion and in (Figure 7) we can see the pseudocode. The algorithm follows two main steps:

• Removal of triangles cut by edge ab to gain an empty area around the edge (Figure 4b,c)
,
• Triangulation of the previously created area, so called pseudo-polygons (Figure 4d)
.

Adding the edge to resulting triangulation is nothing but marking them as fixed, so they become a part of triangulation and cannot be changed. This task is not exposed as one of the steps.

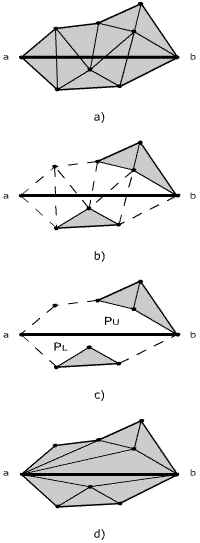
Figure 4: Situation before insertion of edge ab(a), removal of intersected triangles (b) forms two pseudo-polygons P_U and P_L (c) and triangulation of P_U and P_L (d).

2.2.1. Removal of intersected triangles

At the beginning, the first triangle must be located. This is done in constant time, because we know which vertices define our edge, thus we can immediately locate the starting point. Next, we must determine which triangle is the first cut by an edge. We know that one vertex can belong to more than one triangle. So during the process of insertion of points, triangles are built, and every point is equiped with a list of surrounding triangles. Figure 5 shows the searching method. For each overpassed triangle, intersection between inserted edge and edge laying opposite to starting point, is checked. If they do intersect, our search is completed.

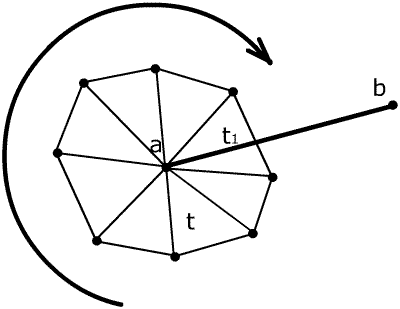
Figure 5: Cycling through surrounding triangles until the first triangle is found, in our example triangle t₁.

Now, ground for triangle removal has been arranged. Moving through triangles is simple (Figure 6). To perform this task, the proposed functions OpposedTriangle and OpposedVertex are implemented.

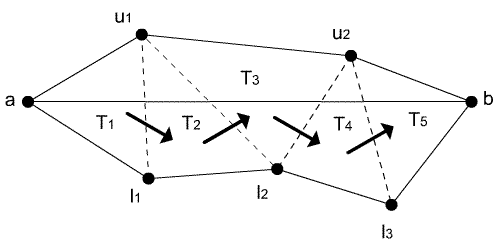
Figure 6: Moving through triangles is stressed by arrows.

Procedure InsertEdgeCDT(T:CDT, ab:Edge)
{Precondition: a,b in(T) and ab not in(T)}
	Find the triangle t in(T) that contains a and is cut by ab
	PU:=EmptyList
	PL:=EmptyList
	v:=a
	While v not in t do
		tseq:=OpposedTriangle(t,v)
		vseq:=OpposesdVertex(tseq,t)
		If vseq above the edge ab then
			AddList(PU,vseq)
			v:=Vertex shared by t and tseq above ab
		Else If vseq below the edge ab then
			AddList(PL, vseq)
			v:=Vertex shared by t and tseq below ab
		Else {vseq on the edge ab}
			InsertEdgeCDT(T, vseqb)
			a:=vseq
			break
		EndIf
		Remove t from T
		t:=tseq
	EndWhile
	TriangulatePseudoPolygon(PU,ab,T)
	TriangulatePseudoPolygon(PL,ab,T)
	Reconstitute the triangle adjacencies of T
	Add edge ab to T
	Mark the edge ab from T as fixed
EndProc

Figure 7: Algorithm for edge insertion

Let us look at the triangles T_papbpc and T_pbpcpd in Figure 1b. If function OpposedTriangle receives a triangle T_papbpc and vertex p_a as arguments, it returns a triangle T_pbpcpd. In case OpposedVertex is called by triangles T_papbpc and T_pbpcpd, vertex p_a of the first entered triangle is returned. Implementation is simple, because it uses links between triangles (every triangle "knows" his neighbours).

When triangle is deleted, all links must be updated. During this process, all points above and below edge are stored separately in two lists, P_U and P_L (Figure 4). Together with the edge, they present pseudo-polygons that must be triangulated.

2.2.2 Triangulation of pseudo-polygons

Triangulation of pseudo-polygons (see pseudocode in Figure 10) is based on strategy "divide and conquer" (Figure 8). The main idea is to triangulate the both upper and lower polygons and link them when finished. As pseudocode shows, we go through all vertices of polygon and check the empty circumcircle criterium for each possible triangle, formed by visited vertex and edge. The checking ends when criterium is satisfied. If currently selected point is p, then p divides the polygon into left and right sub-polygons, which are again recursively triangulated. Recursion stops when a polygon, containing only three vertices, is reached. Trivially, a triangle is constructed and added to triangulation (it must be linked with its neighbouring triangles). These steps are repeated until the whole polygon is triangulated.

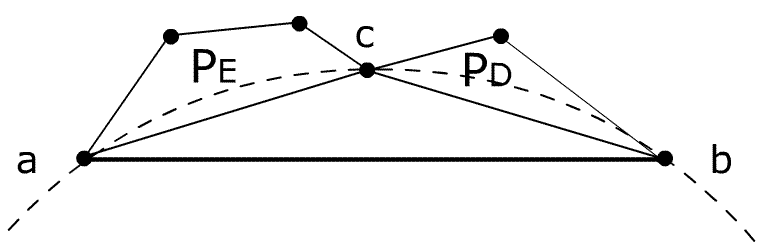
Figure 8: Triangulation of pseudo-polygon: Triangle T_abc fulfills Delaunay criterium, so point c divides polygon into P_E and P_D.

When inputing data, it can sometimes occur, that a point falls directly on the edge. So pseudocode is slightly improved, compared to Anglada's [8], because it can handle such cases. Point {p} appears to split the edge ab, so the algorithm presumes the same. Recursively, it calls a procedure for edge insertion again, yet with a new edge pb (edge ab is now treated as ap+pb). Comparisson is shown in Figure 9.

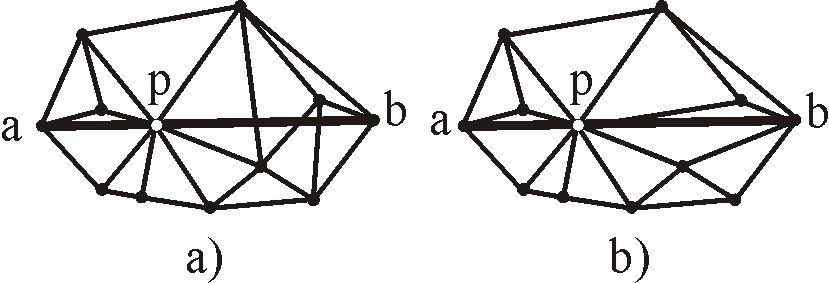
Figure 9: Example shows a situation, where point p falls on the edge ab. In picture a), the situation is not handled, therefore the CDT is incorrect. Picture b) shows our refinement, where edge ab is splitted to new edges ap and pb), both treated separately. CDT is correct.

Procedure TriangulatePseudoPolygon(P:VertexList, ab:Edge, T:CDT)
	If P has more than one element then
		c:=First vertex of P
		For each vertex v $\epsilon$ P do
			If v E CircumCircle (a, b, c) then
				c:=v
			EndIf
		EndFor
		Divide P into PE and PD giving P=PE+{c}+PD
		TriangulatePseudoPolygon(PE, ac, T)
		TriangulatePseudoPolygon(PD, cd, T)
	EndIf
	If P is not empty then
		Add triangle with vertices a, b, c into T
	EndIf
EndProc

Figure 10: Algorithm for triangulation of pseudo-polygon.

I will pass the same conclusions about time complexity for edge insertion and for triangulation of pseudo-polygons as Anglada [8] stated. Let e be the number of triangles of CDT cut by edge ab and m number of edges. The edges are set in a way, that every edge is defined by two vertices which are already in CDT. So finding a starting point a is done in constant time. Number of surrounding triangles can vary between one and maximum, as in the case of the number of edges of convex polygon with a point in the center. Finding the first triangle then requires O(m) time. Construction of upper and lower pseudo-polygons takes a time complexity of O(e²), since in each recursive call, total number of points decreases in one unit. To put all together, procedure InsertEdgeCDT has a worst time complexity of O(n²).

---

3. Results

Several tests have been made on AMD Celeron 1.7 GHz processor with 256 Mbytes of memory on disposal. The operating system was Windows XP.

I tested the algorithm on graphs, using different numbers of points and edges. The procedures for insertion of edges and points were measured separately. Table 1 shows some I observed CPU time in relation with number of inserted edges. Usually, greater number of edges means longer processing. But not always. Another important factor is the number of triangles being cut by edges. Tested example d) has less edges than example e) (Table 1), but takes the same time for edge processing. The reason lies in greater number of removed triangles. Removal itself is not that time demanding. More important is the number of points that compose pseudo-polygons, which is proportional to number of removed triangles.

Figure 11	Edges	Points	Triangles cut	InsertPoint	InsertEdge	Total
(a)	368	1200	988	0.01	0.01	0.02
(b)	4259	1856	1311	0.02	0.02	0.04
(c)	5453	2345	1108	0.03	0.02	0.05
(d)	10000	10000	9462	0.08	0.05	0.13
(e)	13667	6132	2412	0.08	0.05	0.13
(f)	19044	16013	9092	0.211	0.09	0.301

Table 1: Meassured CPU time for tested polygons

Examples in Table 1b,c,e,f present real input data and examples in Table 1a,d are artificially formed and can be seen in Figure 11.

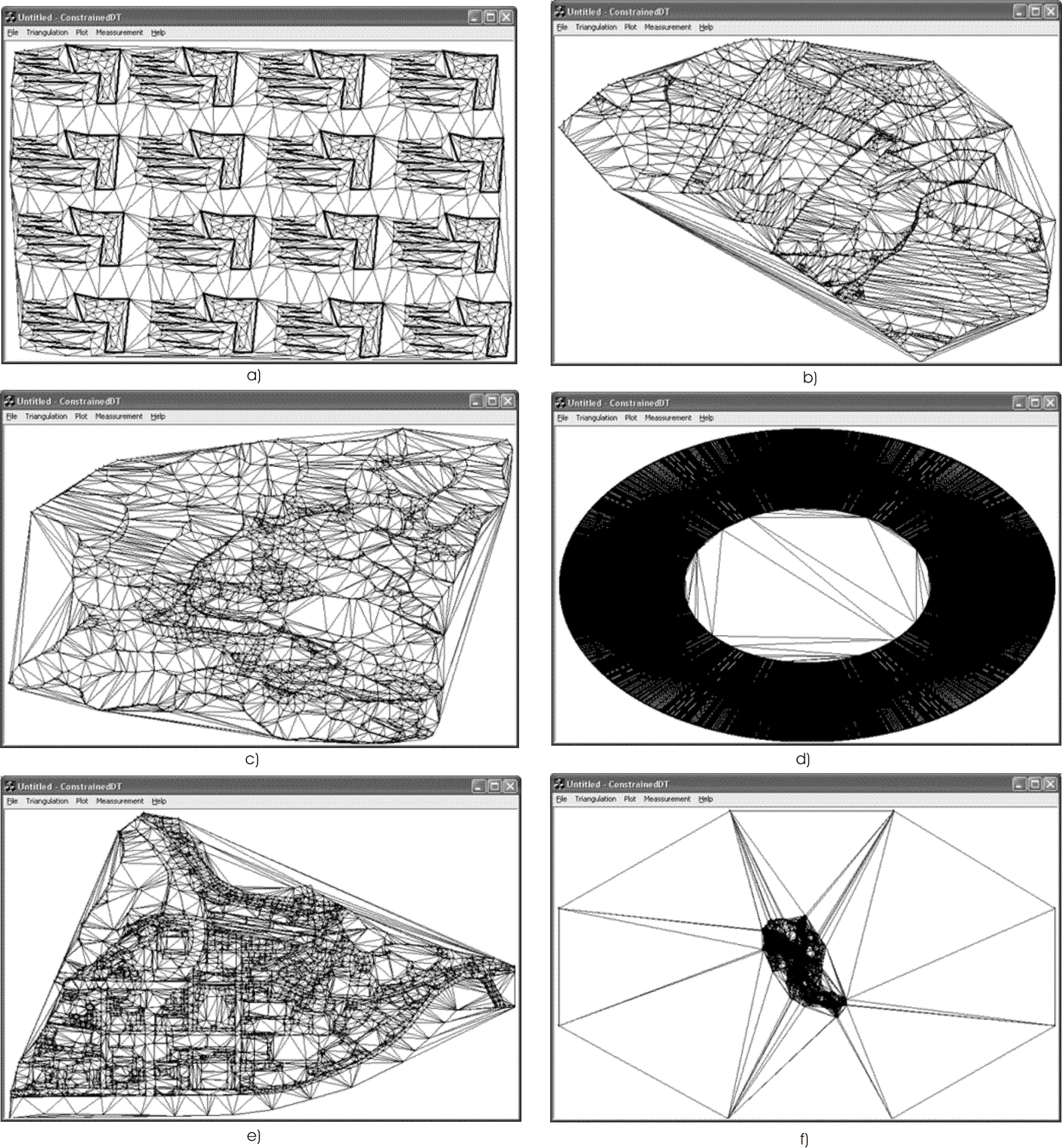
Figure 11: Some tested examples.

---

4. Conclusion

The algorithm copes well with real data and presents a good groundwork for advanced research. The advantages towards other CDT algorithms are especially noticeable in cases of non-uniformally distributed input data. In future, I intend to overcome some disadvantages of the algorithm. When edges are long, relatively to whole triangulation, triangles surrounding them turn out very thin. These triangles are unwanted. One of the ideas is using a polyline that uses triangle edges and tries to fit the inserted edge. Such modification provides a next challenge in my future work.

---

References

[1] Aurenhammer, F., Voronoi diagrams-a survey of a fundamental geometric data structure, ACM Computing Surveys, vol. 23, no. 3, pp. 345-405, 1991.

[2] Chew, L. P., Constrained Delaunay triangulations, Proceedings of the 3rd annual symposium on Computational geometry, ACM Press, pp. 215-222, 1987, Waterloo, Ontario, Canada.

[3] Fortune, S., A sweep line algorithm for voronoi diagrams, Algorithmica, vol. 2, 1987, pp. 153-174.

[4] Guibas L., Knuth D., Sharir M., Randomized incremental construction of Delaunay and Voronoi diagrams, Algorithmica, no. 7, pp. 381-413, 1992.

[5] Hardwick, J. C., Implementation and evaluation of an efficient parallel Delaunay triangulation algorithm, Proceedings of the 9th annual ACM symposium on Parallel algorithms and architectures, ACM Press, pp. 239-248, 1997, Newport, Rhode Island, USA.

[6] Ruppert, J., A new and simple algorithm for quality 2-dimensional mesh generation, Proceedings of the 4th annual ACM-SIAM Symposium on Discrete algorithms, ACM Press, pp. 83-92, 1993, Austin, Texas, USA.

[7] Shewchuk, J. R., Sweep algorithms for constructing higher-dimensional constrained Delaunay triangulations, Proceedings of the 16th annual symposium on Computational geometry, ACM Press, pp. 350-359, 2000, Clear Water Bay, Kowloon, Hong Kong.

[8] Anglada, M. V., An improved incremental algorithm for constructing restricted Delaunay triangulations, Computers \& Graphics, vol. 21, p. 215-223, 1997.

[9] Žalik, B., Kolingerova I., An incremental construction algorithm for Delaunay triangulation using the nearest-point paradigm, Int. J. Geographical information science, vol. 17, no. 2, pp. 119-138, 2003