Introduction Peter Melchart e-mail: e9225615@stud2.tuwien.ac.at

---

1 Abstract * 
2 Terrainfollowing * 
    2.1 General Problem * 
    2.2 Math behind terrain-following * 
    2.3 Simple Approach * 
    2.4 Basic idea of using a grid * 
    2.5 Pseudo-code example * 
3 Collisiondetection * 
    2.1 General problem * 
    3.2 Math behind collision detection * 
    3.3 Simple approach * 
    3.4 Speedups * 
    3.5 Pseudocode example * 
4 References * 

---

1.Abstract 



Building virtual worlds; a topic that brings up some problems one doesn’t think of at the beginning. Beside the usual challenge to make the world as fast as possible ^{[GLAE][WOL94]}, there are some other factors, that make a scenery look real. 

Things like terrainfollowing, collisiondetection and other physical simulations are not hard to implement but have a great effect. Especially terrainfollowing and collisiondetection can be done in a way, which doesn’t cost very much. 

 In the following I try to give an impression how we did it. 
 
2.Terrainfollowing 


 
2.1. General Problem 



When moving through a virtual world, one has the problem to move in a realistic way, but easy to handle. Generally one wants to move left, right, forwards and backwards. The height-level should be calculated automatically (i.e. when walking through a mountain-area). What we also want to achieve is that, when walking up a hill, we’re looking uphill etc. 

That’s basically what terrainfollowing is all about. 

Usually the terrain is build out of triangles, quads, etc. While walking through the scenery it should be detected, on which face the observer is currently located. Then, using vector analysis, the current height level should be calculated. 
 
2.2. Math behind terrain-following 



The following two procedures represent the basic math behind terrainfollowing: 
• Checking whether or not a point is inside of a face:





x0/y0 … point to be tested 

x1/y1 – x2/y2 … line to be tested 

distanceFromLine = x0*y1 + x2*y0 + x1*y2 - x2*y1 - x1*y0 - x0*y2 

If the point lies on the right side of the line, the result is positive, otherwise negative. 

So is we want to check whether or not a point is inside of a face we have to check every edge of a face and look, if that points is right of all edges. 
• Calculating the height value:





Once you know, that you‘re inside of a specific face, the following calculates the appropriate height value: 

px … point1.x 
py … point1.y 
pz … point1.z 

dx1 … point2.x – point1.x 
dy1 … point2.y – point1.y 
dz1 … point2.z – point1.z 

dx2 … point3.x – point1.x 
dy2 … point3.y – point1.y 
dz2 … point3.z – point1.z 

x … object.x 
y … object.y 

l2 = ( ( dx1 * ( y - py ) ) + ( dy1 * ( px - x ) ) ) / 
     ( ( dx1 * dy2 ) - ( dx2 * dy1 ) ); 

l1 = ( x - px - ( l2 * dx2 ) ) / dx1; 

heightLevel = pz + ( l1 * dz1 ) + ( l2 * dz2 ); 

  
• Calculating the pitch
 
For calculating the pitch component in the heading - pitch - roll - vector, you need your position and additionally the heading- value (the rotation angle on the z-axes). With this information you can calculate a point in front of you. Then - calculating the height level of your position and the heightlevel of the point in front of you - you can determine the pitch - angle. 

With that information, it is also possible to do thing like increasing and decreasing speed, stop moving when gradient is too big. 
 
2.3. Simple Approach 



The simplest way to calculate the height is to check all faces that belong to the ground, whether or not we’re inside, and if, calculate the height value. 

// object position: posX, posY 
//  
// 

vector3 position, pointAhead; 

pointAhead = calculatePointAhead ( position ); 

for face = ALL faces IN ground 
{ 
    if ( insideOfFace ( face, position ) ) 
    { 
        positionHeight = calculateHeight ( face, position ); 
    } 

    if ( insideOfFace ( face, pointAhead ) ) 
    { 
        pointAheadHeight = calculateHeight ( face, pointAhead ); 
    } 

    pitchAngle = calculatePitch ( positionHeight, pointAheadHeight ); 
} 

Of course this isn’t a very smart way, ‘cause you have to test every face twice (the position and the position ahead), which usually results in an unacceptable calculating time. 

Thus the question must be how to reduce the faces to be tested. Having a scenery, where all ground faces have the same size, the easiest way is to check the distance from one point of a face to your position, and if it’s too high, skip that face. 

But using that method, you can only save the calculation stuff (calculateHeight, insideOfFace,and ..). You still have to check every face. 

  
2.4. Basic idea of using a grid 



The main problem in reducing face-checks is to determine, which faces are near the object position. We have to develop a way to access a list of relevant faces in a fast way. Of course it is not possible to calculate this list in real-time, so you have to do some precalculations. 

The idea is, to build up a grid, where every grid-entry holds a list of the faces lying on that grid-area. 
int numX, numY; // number of grid - entries in x and y - dimension 

typedef struct 
{ 
    face **faceList; // a list of pointers to  
                     // faces "on" that grid-entry 
    short numFaces;  // number on faces on that grid-entry 
}gridStruct; 

grid = gridStruct [numX][numY]; 

// calulating the dimensions of one grid-entry 
gridLength = sceneLength / numX; 
gridWidth = sceneWidth / numY;  

Once the grid is established, you can easily access a list of relevant faces: 
gridX = (posX - sceneMinX) / gridLength; 
gridY = (posY - sceneMinY) / gridWidth; 

face **faceList = grid[gridX][gridY].faceList; 

So you can get a list of relevant faces with some very cheap calculations: 

Example:  

Lets say we have a scenery, where we have a ground-object with 100 * 100 quads (200 * 200 triangles), which are 40000 triangles. We choose a grid width 50*50 entries, so approximately 16 faces are in each grid-entry. Instead of testing 40000 faces, we only have to test 16 faces which are 0.04%. 

The memory requirement for that grid-structure is about 175KB (2500 entries with a 2-byte short and a 4 byte pointer to a list of 16 pointers (17*4+2 bytes per entry = 175.000 bytes). 

Of course it can happen, that one face is in more than one faceList (intersecting with more than one grid-area). So it could happen, that a list that ideally should have 175KB, has about 300 KB, but I think it pays off. 
 
2.5. Pseudo-code example 
    pointAhead = calculatePointAhead ( position );  

    // getting the faceList for the position 

    gridX = (position.X - sceneMinX) / gridLength; 
    gridY = (position.Y - sceneMinY) / gridWidth; 

    faceList = grid[gridX][gridY].faceList; 
    numFaces = grid[gridX][gridY].numFaces; 

    for face = ALL faces on grid 
    { 
        if ( insideOfFace ( face, position ) )  
        {  
            positionHeight = calculateHeight ( face, position );  
        }  
    }  

    // getting the faceList for the pointAhead  
    gridX = (pointAhead.X - sceneMinX) / gridLength;  
    gridY = (pointAhead.Y - sceneMinY) / gridWidth;  

    faceList = grid[gridX][gridY].faceList;  
    numFaces = grid[gridX][gridY].numFaces;  

    for face = ALL faces on grid  
    {  
        if ( insideOfFace ( face, pointAhead ) )  
        {  
            pointAheadHeight = calculateHeight ( face, pointAhead );  
        }  
    }  

    // calculating the pitch-angle  

    pitchAngle = calculatePitch ( positionHeight, pointAheadHeight );  
As you can see, the program gets a little longer but way faster. 
 
3. Collisiondetection 


 
3. 1. General problem 
Another problem in realistic virtual worlds is to determine, whether or not 2 objects intersect (collide). It’s clear, that a car shouldn’t be able to drive through a wall, etc. 

The main question is how to compute that 2 objects are intersecting. 

There are several ways to achieve this: 
 
• simple bounding box check ^[ZEIL94]
• bounding sphere check
• extended bounding box check
• face level check
• collision object check (VRML proxy objects ^[MARR])

1. Simple bounding box / bounding sphere check 

The simple bounding box and the bounding sphere check are based on the same idea: 

• Calculate the bounding box/sphere once, when the object is generated.
• when the object moves, move the box/sphere along
• test the box/sphere with other boxes/spheres ( very fast )
 
That’s the fastest way to determine a collision. However, this method brings along some tricky problems: 

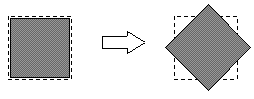Figure 3-1 

Bounding box: As long as objects are only moved and not rotated, everything works fine. But when an object is rotated, it usually leaves its bounding box.(Figure 3-1 ) To solve that problem, we have to calculate the bounding box every time the object changes. But of course that unacceptable. 
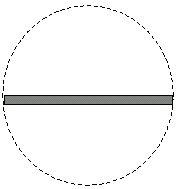Figure 3-2 
Bounding sphere: bounding spheres generally have the problem, that they are only optimal for spheres. Any other object causes a too big bounding sphere (Figure 3-2). 

2. Extended bounding box check 


The idea of the extended bounding box check is to calculate the bounding box once, and then - when transforming the object - use the same transformation matrix on the bounding box. This results in a bounding box with edges that are not parallel to one of the axis (x-, y- or z-axes). 

That means, that there’s the necessity for an extended test. Usually the bounding box is treated like a simple object and is tested on face level with other bounding boxes. 
3. Face level check 

That’s the most general case. Test every point of the first object with every face of the second object and vice versa. See chapter 2.2 
4. Collision object check 

The idea of the collision object is simple. Bounding boxes/spheres are not precise enough, and checking on face level is too slow. So what, if we can provide an object, which is a simplification of the real object, which is not displayed, but only used for the collision check. 

3.2. Math behind collision detection 

 
Before using any intersection algorithm, we need additional information for every face. 

 
1. Plane info 


// calculate normal vector  

vector1 = point1 – point0 
vector2 = point2 – point0  

normalVector = crossProduct ( vector1, vector2 ); 

// calculate plane constant 

planeConstant = dotProduct ( normalVector, point0 ); 

 
2. Inside of halfspace 
  
// calculate whether or not a point lies inside a halfspace of a face 

// the point lies in the halfspace of the face, if 

  

dotProduct (normalVector, point) > planeConstant  


This calculates if a point lies inside the halfspace spanned by a face. This formula needs the normal vector and the plane constant of the face. 

 

Note that the result depends on the order of the points of the face (i.e. clockwise or counter clockwise). 

3.3. Simple approach 

 

For our simple approach we choose the extended bounding box test. Which means we have to compare every pair of objects whether or not they intersect. 
for object1 = ALL objects in scene 
{ 
    for object2 = ALL objects in scene 
    { 
        if object1 <> object2 then 
        { 
            if extBBoxCheck ( object1, object2 ) = TRUE 
            { 
                    doCollisionJob 
            } 
        } 
    } 
} 

As you can see we have costs order n². 

So we have to think about the following questions: 

 
• How can we reduce the objects to be checked? and
• What kind of test do we use?

3.4. Speedups 

There two speedup methods, I want to talk about. 
 
• collision groups
• LOD collision check

1. Collision groups



Let’s assume we have a scenery with a road, some cars, trees and some airplanes flying around in the air. Usually cars can’t fly and airplanes don’t drive on highways so it’s of no use to check the airplanes with the cars. Also you cannot really collide with the ground (the ground object(s) are checked using terrainfollowing). So it would be pleasant, if we would check only objects, that actually can collide. 

The easiest way is to define some collision groups. Objects can only collide, when they are in at least one common group. 

Let’s define some groups: 
 
• Ground objects
• Vehicles
• Trees
• Stones
• Air objects
• Airplanes
 
Every car is in the group vehicles and in the group ground objects. 
Every airplane is in the group airplanes and in the group air objects. 
Trees are in ground objects and in trees. 
Rocks are in Stones. 

So in that example an airplane can’t collide with a car, ‘cause they have no common group. 

Let’s say, we have a ghost walking around in our scenery. If we want him let collide with trees and rocks, but not with cars, we put him in the group trees and stones. Putting him only in the group ground objects would let him collide with cars, too. 

We implemented the groups with a bitfield, where every bit represents one group (so there’s a maximum of 16 or 32 groups). Thus the test if two objects have one common group is simply one bit-AND of the bitfields of the two objects. 
2. LOD collision check



When two objects are checked for collision, it is absolute useless to perform always the face level-check. Also it is not very satisfying to all objects only on bounding box level. This cognition leads us to the idea to perform several levels of tests. 

When we want to test two objects, we have to: 
 
1. check for common collision groups
2. if more than one group is common: check extended bounding boxes
3. if intersection: perform face level check / collision object check
 
In the most cases it’s precise enough to perform steps 1 and 2. 
3. 5. Pseudocode example 
 

for object1 = ALL objects in scene 
    for object2 = ALL objects in scene 
        if object1 ¹ object2 
        { 
            if object1 is in a collision group  
            { 
                if extBBoxCheck ( object1, object2 ) = TRUE 
                { 
                    if faceLevelCheck / collisionObjectCheck ( object1, object2 )  
                       = TRUE 
                    { 
                        doCollisionJob 
                    } 
                } 
            } 
        } 
  
As you can see, it’s still necessary to check every object with every other object. 

To avoid this, we could build up al list for every collision group. So every object has to be tested only with that objects it’s in the same group with. 

4. References 

[GLAE]  Glaeser Georg: "Fast algorithms for 3D graphics" Springer - Verlag, 1995 

[WOL94]  Wolberg George: "Digital image warping" IEEE-Press, 1994 

[ZEIL94]  Zeiller Michael: "Collision detection for complex objects in computer animation". Dissertation at the Technical University of Vienna, July 1994 

[MARR]  Marrin Chris "VRML2"