![[CESCG logo]](../../CESCG/images/cescg98.small.gif)
Jana Pilnikova, Jaroslav Placek, Juraj Sofranko
3pilnikova@st.fmph.uniba.sk, Jaroslav.Placek@st.fmph.uniba.sk, Juraj.Sofranko@st.fmph.uniba.skFaculty of Mathematic and Physics
University of Comenius
Bratislava, Slovakia
![[CESCG logo]](../../CESCG/images/cescg.small.gif)
![[CESCG logo]](../../CESCG/images/cescg98.small.gif)
|
Polar Forms and Geometric Continuity of Surfaces
Jana Pilnikova, Jaroslav Placek, Juraj Sofranko 3pilnikova@st.fmph.uniba.sk, Jaroslav.Placek@st.fmph.uniba.sk, Juraj.Sofranko@st.fmph.uniba.skFaculty of Mathematic and Physics University of Comenius Bratislava, Slovakia |
![[CESCG logo]](../../CESCG/images/cescg.small.gif)
|
Abstract
The paper is concerned about the question of smooth glueing of triangular Bézier patches. In the beginning polar forms are briefly explained. After that they are applied on parametric continuity. We'll obtain a geometric interpretation of C
1 and C2 smoothly joined Bezier patches.In the next part we'll deal in geometric continuity. We will show relations between derivatives of two maps which are forced by the condition of their geometric continuity. In the place of shape parameters matrixes occur. The remaining part of the work is devoted to investigating of these matrixes and reparametrization functions. It seems that the matrixes are not arbitrary but very strong condition are put on them.
Let points t0,t1,t2 Î E2 are non-colinear. Then for each u Î E2 there exist unique triplet of numbers l0(u), l1(u), l2(u) Î R satisfying
u = l0(u) t0+ l1(u) t1+ l2(u) t2; l0(u) + l1(u) + l2(u) = 1.
The numbers l0(u), l1(u), l2(u) are called barycentric coordinates of the point u with respect to triangle t0,t1,t2.
In the next let's suppose that the points
t0,t1,t2 are fixly given.Polynomial BD ijk : E2 ® R defined
![]()
is called Bernstein polynomial. Notice, that all Bernstein polynomials of degree of n (i.e. i+j+k = n) create the basis of the space of polynomials of degree at most n.
Let B: E2 ® R is defined:
![]()
The restriction of this map to D
t0,t1,t2 is called triangular Bezier patch of degree n. Points bijk are control points and create a control net.
A map f: M ® N is linear iff it preserves the linear combination of vectors, i.e.
f(S a iui) = S a i f(ui); ui Î M, a i Î R
f: M ® N is affine iff it preserves the affine combination of points:
f(S a iui) = S a i f(ui); ui Î M, S a i = 1, a i Î R
f: (M) n ® N is multilinear (multiaffine) iff it is linear (affine) in each of its arguments when the others are fixed.
f: (M) n ® N is symmetric iff its value does not depend on the order of arguments. It means
f (up 1, up 2, . . . up n) = f (u1, u2, . . . un)
where (p 1, p 2, . . . p n) is a permutation of the set (1,2, . . . n).
Now we can approach a definition of polar forms.
Let F is polynomial E2 ® Ed of degree n. Then there exists unique map f: (E2) n ® Ed which is multiaffine, symmetric and has a property of diagonal, i.e. f (u, . . . u) = F(u). This map is called (affine) blossom (polar form) of F.
For our cogitations linear blossoms are more useful. For this purpose we must present this two special insertions E2 to E3.
u = (u1, u2) Þ uÙ =(u1, u2, 0)
u = (u1, u2) Þ u- =(u1, u2, 1)
Linear blossom ( polar form) of the polynomial F: E2 ® E3 is a map f*: (E3)n ® Ed which is multilinear, symmetric and has a property of diagonal, i.e. f*(u-, . . . u-) = F(u). Such map always exists and is unique.
Linear and affine blossoms of the same polynomial F satisfy
f* (u-1, u-2, . . . u-n) = f (u1, u2, . . . un); ui Î E2
Maps F,G :
E2 ® Ed are parametric continuous of the order q in u Î E2 if their directional derivatives in u up to order q are the same.The theory of polar forms can be applied on parametric continuity of surfaces. But first let's mention their two important properties:
Let F be a Bézier patch of degree n with control points
bijk for i + j + k = n with respect to D t0,t1,t2 and let f be its polar form. Thenbijk = f (ti0,tj1,tk2); i + j + k = n
Furtehmore if we denote Dx 1x 2... x k F(u) q-th directional derivative of F in u with respect to vectors x 1, x 2 . . . x q then the linear blossom of F: E2 ® Ed satisfy relation
![]()
where f
* is the linear blossom of F. Proofs of these properties you can find for example in [3].We started to use a simpler an lucider multiplicative notation:
Instead of f
(u1, u2, . . . un) we are going to write f (u1 u2 . . . un). By the entry f (un-k u1 u2 . . . un) we want to say that argument u occurs (n - k) times there.Therefore, if we want to find out a vallue of a derivative of a polynomial we don't need to derive but it is enough to look at a certain value of its blossom.
From the previous theorem we get conditions for parametric continuity of two patches.
Let F,G :
E2 ® Ed are triangular Bezier patches and let u be a point from E2. Then according to (1) F and G are continuous in u of order q ifff* (u- n-ix 1 . . . x i) = g* (u- n-i x 1 . . . x i); i = 0, ... q
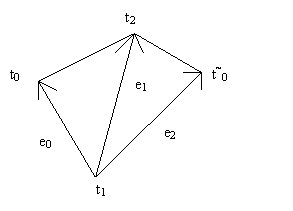
Figure 1: Mapped space
Let's denote barycentric coordinates of t
~0 with respect to D t0,t1,t2 as l0, l1, l2 :t
~0 = l0 t0 + l1 t1 + l2 t2, l0 > 0. Let Bézier patches F,G map this point configuration in this way:F : D
t0,t1,t2 ® E2G
: D t~0,t1,t2 ® E2Further let
bijk are control points of the patch F and b~ijk are control points of the patch G. Let's investigate a continuity of these two patches along the common edge t1t2. If we suppose Co continuity, it is obvious, that derivatives in u Î t1t2 with respect to e1 are the same - it is the same Bezier curve. So that it is enough to find only one more direction which is lineary independent with e1 with respect to which the maps F,G poses the same derivative. Then the C1 continuity is satisfied because of the fact that Dx F(u) is linear in x for a fixed u and so the other directional derivatives can be composed from the mentioned two.We can write:
t~0 - t1 = l0 (t0 - t1) + l2 (t2 - t1)
e2 = l0 e0 + l2 e1
D
e2F(u) = l0De0F(u) + l2De1F(u)De2G(u) = De2F(u)
De2G(u) = l0De0F(u) + l2De1F(u)
g*(u- n-1e2Ù ) = l0 f*(u- n-1e0Ù ) + l2 f*(u- n-1e1Ù )
. . . . .
g(t~0,t1i,t2j) = l0 f (t0,t1i,t2j) + l1 f (t1i+1,t2j) + l2 f (t1i,t2j+1)
b~ijk = l0 b1 i j + l1 b0 i+1 j + l2 b0 i j+1 ; i + j = n, u Î t1t2
And thanks to the blossoming we have simply obtained well-known geometric interpretation of the C
1 continuity:Bézier patches F : D
t0,t1,t2 ® E2, G : D t~0,t1,t2 ® E2 are C1 smoothly joined along the common boundary iff the control points b1ij, b0 i+1 j, b1ij, b0 i j+1 lay in the same plane and create an affine image of the quadrangle t0t1t~0t2.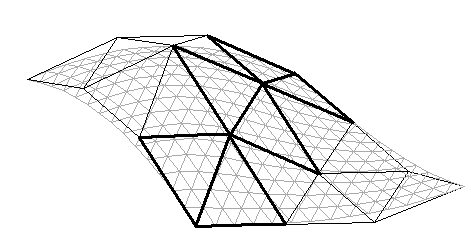
Figure 2: Geometric interpretation of C
1 continuityAfter similar cogitations we can obtain not so known geometric interpretation of C
2 continuity:Bézier patches F : D
t0,t1,t2 ® E2, G : D t~0,t1,t2 ® E2 are C2 smoothly joined along the common boundary iff moreover there exist points di; i=1, .... n-1 such that vertexes b2ij, b1 i+1 j, di, b1 i j+1 lay in the same plane and create an affine image of the quadrangle t0t1t~0t2 and also points di, b1 i+1 j, b2jk, b1 i j+1 are coplanar and create an affine image of the quadrangle t0t1t~0t2 too.

Figure 3: Geometric interpretation of C
2 continuity
Let F, G :
E2® Ed are maps. Let u Î E2. Then F, G are in u geometric continuous of order q iff there exists such parametrication of surfaces F, G that they are parametric continuous of order q. It means:F = F(x,y) i.e. is a function of parameters x, y
G = G(s,t)
Let's try to reparametrize the map F and express it by s, t. So x and y will be written as functions: x= x(s,t), y = y(s,t). Let both maps are now expressed in the way that they are parametric continuous in u = (s
0, t0):Continuity of the first degree:
F
s(u) = Gs(u) Ù Ft(u) = Gt(u)For continuity of the second degree moreover
F
ss(u) = Gss(u) Ù Fst(u) = Gst(u) Ù Ftt(u) = Gtt(u)But F has to be derivated as a compound function. Let's denote
![]()
Then the relation between derivatives of F and G with respect to the original parameters can be expressed by connection matrices
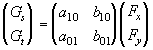
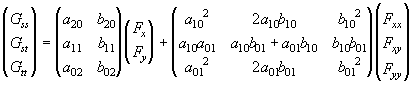
Let G' is the matrix of first derivatives of G, G'' is the matrix of its second darivatives an so on. Similary let F' is the matrix of first derrivatives of F, F'' is the matrix of its second derivatives and so on. Then the relations (2), (3) and other can be written in a simpler way:
G' = W
11 F 'G'' = W 12 F ' + W 22 F '' (4)
G''' = W 13 F ' + W 23 F '' + W 33 F '''
Surfaces F and G are in u geometric continuous of degree q iff there exist matrices
W ij ; j = 1 . . . q, i = 1 . . . j
satisfying the mentioned relations.
We observe that the relations for the geometric continuity of surfaces are very similar to the ones for the geometric continuity of curves. But as a shape parameters there are matrixes W ij instead of real numbers.
Now we are going to apply the results of the previous section on the Bézier patches. Let Bézier patches F, G are defined on the quadrangle t
0t1t~0t2 like this:F : D
t0,t1,t2 ® E2G
: D t~0,t1,t2 ® E2Let F and G are regularly parametrized in this way:
F = F(r,s)
G = G(s,t)
where parameter r raises in the direction e
0, s raises in the direction e1 and t in the direction e2 (look fig.1). We suppose Co continuity F(0,b ) = G(b ,0). In the beginning we require geometric continuity of the first order of the patches F and G along the common boundary t1t2. It means that for all u from this edge there exist a matrix W 11 satisfying (2). In this special case it can be written:![]()
where a
ij, bij are functions of the point u.Thanks to the fact that parameter s is common for both F and G it holds D
e1G(u) = De1F(u) for all u Î t1t2 and so a10 = 0 and b10 = 1 constantly.Let a = a
01 b = b 10 for simplicity. Then:
The result can be geometricaly interpreted: Bezier patches are in u geometric continuous of the first degree iff they have in u the same tangent plane.
Let's continue by investigating the geometric continuity of the second degree of two Bezier patches. Besides the matrix W
11 with the specified form the matrices W 12 and W 22 must exist such thatG'' = W
12 F ' + W 22 F ''If we look at (3), we can notice that all the elements of the matrix W 22 are already known because it is composed only from coeficients occured in W 11.
And as for W 12, it's possible to proceed like in the case of W 11. Because the same parameter and the derivative of the same curve is considere, it holds
De1e1G(u) = De1e1F(u) Þ a20 = b20 = 0
It will be a bit more complicated for the combined derivatives:
De1e2G(u) = De1(De2G(u))
= De1(aDe0F(u) + bDe1F(u))
= aDe1(De0F(u)) + bDe1(De1F(u))
= aDe0e1F(u) + bDe1e1F(u)
and after comparing with (3) we obtain a11 = b11 = 0 constantly fo all u Î t1t2.
The result of this observations is the next equation:
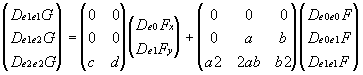
We could continue similary. After the small cogitatation above the equation for the q-th derivative
G
(q) = W 1q F ' + W 2q F '' + . . . + W qq F (q) (5)we realize that if the previous derivatives has been invastigated, new coeficients appear only in matrix asdfasdf - the q-th derivatives of the reparametrization functions are only there. Let's look at it more closely.
Let the reparametrization functions x and y are polynomials of degree m (look[2]):
![]()
From the matrix W
12 it follows xuv = a11 = 0 and also yuv = b11 = 0. It means that nor x(u,v) neither y(u,v) contains combines member. Furthermore from W 11 it is xu = a10 = 0, i.e. x doesn't depend on parameter u. In the case of y it is a bit different: yu = b10 = 1 constantly along the whole boundary t1t2. It means that y(u,v) contains u only as a linear member with coeficient 1. The result can be written:![]()
And then we obtain more specific form of W
1j: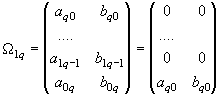
Let's look at the result. It seems that if the conditions of GC
q-1 smooth joining of the patches F and G has been formulated and we want to reach smoothness of q-th order, it can be determined by only two shape parameters in the matrix asdasd. There's no possibility to manipulate with other matrixes occured in the relation between G(q) and F(q) (look(5)). So the geometric continuity of curves and surfaces are very similar not only because of the form of the equation system(4) but also because of the constraints for the work with shape parameters.[1] J. M. Hahn: Geometric Continuous Patch Complexes. Computer Aided Geometric Design, (6):55-67, 1989.
[2] J. Hoschek, L. Dieter: Fundamentals of Computer Aided Geometric Design, pp. 330-370, A K Peters, Ltd, 1993.
[3] H. P. Seidel: Polar Forms and Triangular B-spline Surfaces. Computing in Euclidian Geometry, pp. 235-286, 1992.