![[CESCG logo]](../../CESCG/images/cescg98.small.gif)
Marek Zimanyi
Department of Computer Graphics and Image Processing
Comenius University
Bratislava, Slovakia
![[CESCG logo]](../../CESCG/images/cescg.small.gif)
![[CESCG logo]](../../CESCG/images/cescg98.small.gif)
|
Reconstruction of Tomographic Data by Markov Random Fields
Marek Zimanyi Department of Computer Graphics and Image Processing Comenius University Bratislava, Slovakia |
![[CESCG logo]](../../CESCG/images/cescg.small.gif)
|
| The most important part of 3D visualization of tomographic data is an object model reconstruction. The traditional reconstruction techniques include some artefacts since the distances between slices are too big. We cannot scan the CT slices of smaller distance due to either the radiation dose or the time.We have developed a new statistical reconstruction technique based on both data modelling by Markov random fields and finding solution by Simulated annealing algorithm. |
![]() Modeling data object by Markov Random
Fields
Modeling data object by Markov Random
Fields
CT scanner provides an information about scanned
object, which is put in set of 2D projections-two dimensional pictures,
slices. This slices are saved in a digital form and ready for other use.
Visualization is a very important part of CT slices
processing. This scanned data visualization might be based on simple display
of single pictures or on a more difficult reconstruction of a 3D object
model. We are particularly interested in this second part of the CT slices
visualization.
Traditional interpolation techniques contain many
different artifacts (postaliasing, prealiasing, ringing ...), which arise
while scanning an object (noise) or during the reconstruction itself. This
artifacts depend on the size of interval the object was scanned within.
It was a reason which led us towards the idea of creating a new reconstruction
technique. This technique suppresses previously mentioned artifacts and
uses parameters obtained from CT scanner.
The main goal of our work is to introduce a new
statistical reconstruction technique which uses both Bayesian paradigm
and data modelling by Markov Random Fields (MRF) tomographic data processing.
A new consequential model is created according to the qualities of CT scanner
and scanned data. Our program interpolates data with this new technique.
We transform the reconstruction problem of 3D object
to the 1D object reconstruction. This 1D object is a perpendicular line
on slices ( figure 1a ). A value of any pixel
of this line is a value of the function in this point (figure
1b, c).
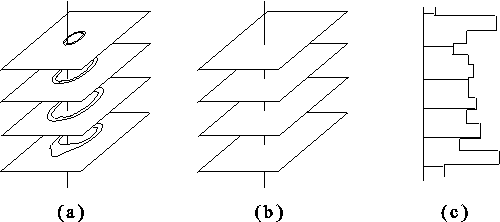
Modeling data
object by Markov Random Fields
We express relationship between scanned data and the set of values
f by Bayes formula [Li]:
p(f):
From Markov
random fields theory we can express a priori probability
p(f) as
p(f / d):
Since p( d ) is fixed for "
f Î L (set of all
values model f , 256 level of greyscale) we can express solution
f*as
We use Simulated
Annealing (SA) [Li] for minimalization of the energy E(f).
SA simulates the physical annealing procedure in which a physical substance
is melted and then slowly cooled in a search of a low energy configuration.
For the escape from the local minimum to the global minimum the Metropolis
algorithm is used. At each step the following configuration f'
is randomly chosen from N(f) ( the vicinity of f ),
for instance, by changing one of the fi's into a new
label fi'.
Metropolis:
initialize f,
repeat
generate f' Î N(f);
DE ¬ E(f') -
E(f);
P = min{1, e-DE/T};
if random á0,1) < P then
F ¬ f';
until (equilibrium is reached)
return f
SA applies a sampling algorithm, Metropolis, successively at the decreasing values of the temperature T. The starting temperature is choosen from Metropolis algorithm: T is the start temperature when number of accepted statuses is 70 - 80%. Number of iterations we can choose 10n or 5n, where n is a number of sites. The decreasing sequence of temporary must satisfy limt -> µ T(t)=0. So T(t) we can choose as T(t)=(C / ln(1+ t)) or T(t) = kT(t-1).
Simulated Annealing:
initialize T=Tmax
and generate f
repeat
Metropolis(T,f);
decrease T;
until (T > Tmin)
return f
The parameters of CT scanner are thickness and radiation intensity. We can express these parameters by the Point Spread Function (PSF). The x axis is perpendicular on CT slice and axis y is paraller to it. Scanned material is a plate with the thickness w and with the inclination 45o according to the plain of scanning. y axis goes through the slice and x axe is perpendicular on y, and goes through the first intersection of the material with y axis.
We examine an intensity of scanned point in y0.
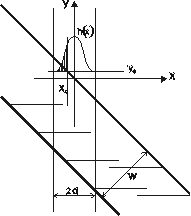
But the function f(y) on interval <-d,d>
is discrete and so we can substitute f(y) by the set of values
We choose an approximate function (e.g. Gaussian) from these points or we use directly these points.