Collision Detection and Impulse Dynamics in Real time Applications

Petr Sovis

xsovis00@dcse.fee.vutbr.cz

Faculty of Electrical Engineering and Computer Science

University of Technology

Brno / Czech Republic

1. Abstract

The computers are getting more powerful and the 3D applications and games are getting more sophisticated and therefore there is a need to make applications more realistic with keeping speed of application. This can be done by using real-time physical simulation system but it is not without some accuracy degradation. In order to assure hight degree of realizm as well as to maintain high performace of our graphic engine we must choose an efficient and robust collision detection algorithm and the method for solving dynamic behaviours of modelled objects in the scene.

Keywords: closest feature, V-region, collision detection, collision state, multi-point collision, sliding mode, resting mode.

Introduction

There are two different approaches of doing physic simulation. You can choose between impulse based approach and constraint approach. The impulse based simulation describes object behavior like in normal world. Whole simulation time is divided into single steps, which are constant or various portions of time and each step you integrate objects along theirs trajectories, you detect all collisions in step. Then it must be merged and the first collision is solved and impulse of collision contact is applied on both objects. Then you must reset collisions, decrease portion of time in current step and look for next collision. When all work in step is done, you can draw current positions of objects and continue solving next time step. In other hand the constraint simulation is based on collecting all collisions and impulses acting on object and solving equations system. This approach can be faster but there are some problems (equation system is hard to solve when you want to use friction and other physic simulation laws in collision response).

To make your system real-time, some inaccuracy in solving collision response and integrating objects along theirs trajectory is needed. Fast collision detection is needed as well. In next chapters I am going to describe, how to make simulation real-time.

2. Collision detection

The base of physic simulation is in real-time collision detection. Most of computing time is spent in collision detection and then the collision detection must be very fast and very precious. These conditions are satisfied by some of closest features collision algorithms. My solving is based on V-clip collision system [1]. This system is very easily updated to detect multi point collisions and therefore you can solve more collision states.

Object is assembled from vertexes, edges and faces. Each of these parts is basic feature and each feature has a subspace bounded by surfaces. These subspaces are called V-regions. All V-regions covers whole area around object and are not intersected. This means, that point outside object belong to one and only one V-region of object – and therefore point outside object points to only one feature on object (to whom V-region point belongs). This feature found on object is the closest feature on object to point.

The important thing is to save neighborhood of features. Face is assembled from edges and therefore face has edges as neighbors. Each edge has two vertexes and two faces as neighbors. Each vertex has as neighbors all edges leading into him.

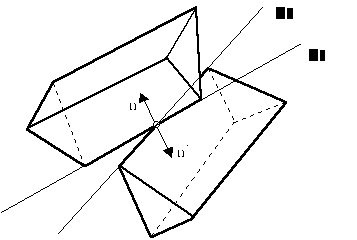
How to create V-regions to faces, edges and vertexes of object? Surfaces of V-region of face are created from edges of surface and are perpendicular to face it belongs. V-region of edge is created from 2 surfaces of neighboring faces and from surfaces created from directive vector of edge and points of edge. V-region of vertex is created from surfaces bounding neighboring edges. The creation of V-regions of features is shown on next picture .

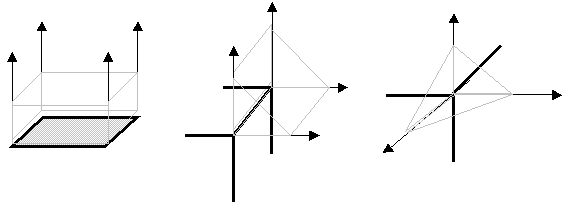
Figure 1

If you create V-regions of all features in object, you can solve main closest-feature searching algorithm. The output of algorithm is pair of 2 closest features (one feature on each object). If you can see, the algorithm can be in 5 states, depending on current features on objects. States can be Vertex-Vertex, Vertex – Edge, Vertex – Face, Edge – Edge, Edge – Face. Other states are not enabled, because is not possible to get in these states. The algorithm is based on tracking along objects and searching if the neighbor feature is not closer than actual one. If it is, the current feature is updated to closer one. If no closer feature is found, the algorithm ends and the current pair of feature is result. The power of this algorithm is that it never cycles between two features and always ends even in states of penetration. The updates of current pair of features is not simple and each state needs special solving. For example state vertex-vertex: Assign current vertex of object 1 as V1 and current vertex of object 2 as V2. Then search if V2 lies behind at least one surface of V-region of V1. If it is true, feature V1 is updated to neighbor edge corresponding to surface of V-region of V1 that V2 is lying behind. If it is false, take V2 and test the same for V1’s V-region surfaces and update features in the same way. Other states are more complicated and the complete solution is in [1].

Furthermore the algorithm returns the closest pair of features on both objects you are testing against collision. Even in penetration states, the return is correct. Than you can extend algorithm with other features. The algorithm returns only these combination of pairs: Vertex –vertex, Vertex – edge, Vertex – face, Edge- Edge, however the real collision occurs only in two states: Vertex – face and Edge-Edge states. Other states aren’t real collision, but you must handle these states.

2.1 Collision response

As it was said, you can obtain four states from collision detection. We always solve collision response of two objects as collision of face and vertex and other states of collision we must convert into this state. Next pictures show the conversion of other states and also response in common state – Vertex –Face.

2.1.1 Vertex-Face collision

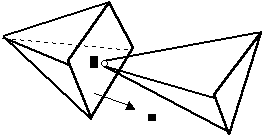
Figure 2

The most interesting thing of collision detection is point of collision P and normal of colliding face n.

2.1.2 Vertex – Vertex collision

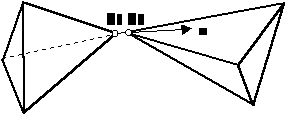
Figure 3

colliding vertexes (P1 of Object1 and P2 of Object2) creates surface of normal n (equal to vector P1,P2) and collision point (one of P1,P2 or average of P1,P2)

2.1.3 Vertex – Edge collision

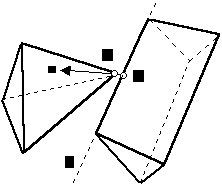
Figure 4

To solve this state you must find the closes point X on edge E to vertex V. If you have done it, you can make normal of collision n = X – E and point of collision one of E,X or average of them.

2.1.4 Edge –Edge collision

Figure 5

You must find one of the closest points on one edge to another (X on E1 closest to E2 or X on E2 closest to E1). Then you have point of collision. The normal of collision n is vector multiplication of directional vectors of E1 and E2, but you must be sure that the vector n leads from basic collision edge to other edge (vector multiplication can give result in both directions, but only one is correct). For example you have E2 as the base edge. Then you obtain by vector multiplying n or n’. To choose the correct one test the n and n’ against normal of one of neighbor faces of E2 – F1 or F2. The angle of n,F1 and the angle of n,F2 must be less than 90 degrees (applying scalar multiplication ).

After this processing you have collision normal n and collision point P. Then you can solve collision by the common way. The impulse separating both objects from each other acting in collision normal n and his value is j. You can solve j in this way (summarizing results of [BAR])

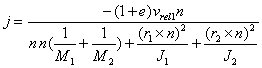
Where:

M1, M2 are the masses of objects,

J1, J2 are the inertia tensors of objects

r1, r2 are vectors from center of masses of objects to colliding point P

e is reflection factor, it can be 0 for no reflection till 1 for perfect reflection

is relative velocity of colliding points of objects

and velocities v1 and v2 are absolute velocities in colliding point for object 1 and object 2. They can be counted from linear velocity of object vlin(t) and angular velocity vang(t) and vector r (point of collision P – center of mass of object).

v(t) = vlin(t) + r(t) x vang (t).

Now apply impulse I = j*n to both objects and obtain new values of linear velocity and angular velocity.

2.2 Collision determination

Even if collision between two objects is determined, it could not be real because the distance can increase – the object is getting farther from other object. Then you cannot apply collision impulse on objects and must leave objects without change. This state can be determined from relative velocity vrel, when vrel < 0. If vrel > 0, then collision really happens.

2.3 Collision time searching

When you do physic simulation you have to know the exact time of collision and you must solve collision before penetration happens. This is a problem, because this searching can never ends. Declare d(t) as the precious minimum distance of two objects, which are colliding in next time. You are looking for the root (zero distance) of function d(t). If it is possible it should be the first root, because the function d(t) can pass zero distance many times. Next picture shows the possible behavior of d(t) in time.

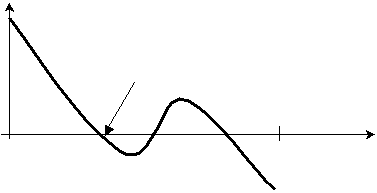d(t)

the root we are looking for

0 dt t

Figure 6

We recognize collision as the state that in t = 0 d(t) > 0 and in t = dt is d(t) < 0. Then you can use standard methods of root finding. From the test the Newton method with some linear correction (10% linear decrement of d(0)) is fast enough. But the problem is, that the collisions can happen shortly after each other. For example ball is between two faces and reflects quickly from one to other. If the ball is the nearly same size as the hole, where it is in, then collisions will come very often. Then system does only integration and even powerful computers slow down. Next problem is, that if you start root finding with d(0) < 0 (objects are in penetration) then the root finding never ends, this mean you must avoid penetrations of objects and always solve collisions in some time before the penetrations happen. These situations are solved by next algorithms.

The root finding is slow, because if you want to get d(t), you must perform collision check and then obtain d(t) from closest features. By establishing collision window you can avoid this situations. Declare 2 different distances form object epsilon1 and epsilon2, where epsilon2 is greater than epsilon1 and both are greater than zero distance. When d(t) of objects is less than espilon2 and greater than epsilon1 than you can solve collision in time t directly, but if the d(t) is less than epsilon1 than you must find t in which d(t) is greater than epsilon1 and is less than starting time t = 0. But this is more simple than root finding in every time collision occurs.

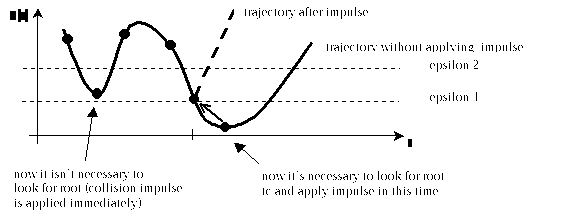
Figure 7

2.4 Multi point collision

Next step of collision response optimalization is to find more than one colliding point. In real situations many collisions are face to face, but the collision detection system cannot return state face-face, so you must append some short code to obtain all point of collision (including collision edge-face, face-face).

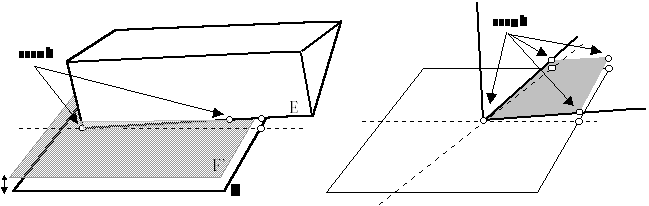
clipping edge E against V-region of F and

against parallel surface F’ in some clipping face determined by 2 edges against

distance k from F, result is edge-face state V-region of face F – result is face-to-face state

Figure 8

From state Vertex-Face test all edges leading from vertex against face of collision and test the angle of normal of face and directional vector of each edge. If angle is less than some constant, than edge lies on face and only work to be done is clip edge against V-region of face and parallel surface to face of collision at some distance (distance k). If more than one edge has angle with face less than constant, than face between edges lies on other face. Than you must clip face against collision face’s V-region and face F’ (face in distance K) and obtain set of collision points.

In that way you obtain complete set of collision points of object and others. The goal of this counting is detection of sliding mode (2 objects are sliding at each other) and detection of resting mode (one object lies on others).

Other goal is in that after applying impulse on every colliding points we separate objects for whole step and other collision in this step cannot occur (because we apply gravity and external force only once per a step). Exception is when other collision throw object back and collision occurs again.

2.5 Resting mode detection

Resting object mode is mode when the object lies on other object (objects). Then you don’t need to recount collisions with objects that object lies on. Realize that object has a center of mass and kinetic energy. When the center of mass and vector of external forces acting on it (like gravity and some other field) points into projections of colliding points and the kinetic energy is less than some value, then object cannot move and can become in resting mode. Resting mode is possible recount after all collisions responses (it is not possible to evaluate it without collision).

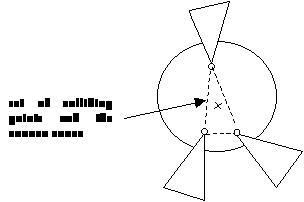
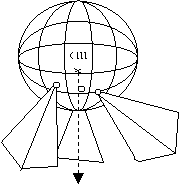
projection from cm

in direction of gravity

gravity

Figure 9 Figure 10

Now it is problem to make convex cover from set of points and determine if center of mass lies inside this convex cover.

3. Conclusions

All these methods are used only as extension of dynamic system and can very faster impulse based simulation, so it can become real-time. But there is more work to do. There must be solved the application of friction in every collision response solving (the friction depends on force and plane of collision), solve resistance of environment acting like an external force maybe behavior of objects swimming in fluids. All of these extensions are very time consuming and must be fast.

4. References

[1] Brian Mirtich: V-Clip Fast and robust polyhedral collision detection, 1997

[2] David Barraf : Rigid body simulation – Unconstrained rigid body dynamics