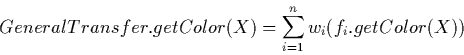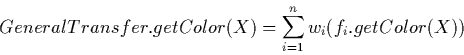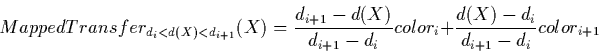

Next: Phase Functions
Up: A Flexible Framework
Previous: Density Functions
Transfer functions in our framework use color-maps as well as special algorithms
like iso-surface or region boundary algorithms to map scalar density values to
renderable properties. Again, only a single interface function is needed -
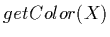 , which
returns a color for each point
, which
returns a color for each point 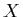 in space, using the underlying density
function. In order to combine different transfer functions, 2 additional
functions, taking transfer functions as arguments and presenting themselves
again as transfer functions, are used.
The first transfer-function-combination-function is called
in space, using the underlying density
function. In order to combine different transfer functions, 2 additional
functions, taking transfer functions as arguments and presenting themselves
again as transfer functions, are used.
The first transfer-function-combination-function is called
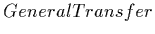 .
It is quite powerful and allows for the
combination of an arbitrary number of transfer functions with associated
weights. The values at each point
.
It is quite powerful and allows for the
combination of an arbitrary number of transfer functions with associated
weights. The values at each point 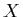 are scaled by their associated
weight and then summed up. The result is a new transfer function which is a
weighted sum of other transfer functions:
are scaled by their associated
weight and then summed up. The result is a new transfer function which is a
weighted sum of other transfer functions:
where 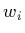 is the weight associated with the i-th density function and
is the weight associated with the i-th density function and 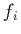 is the i-th transfer function.
The second functions is called
is the i-th transfer function.
The second functions is called
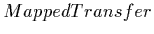 and allows for
the selection of a single transfer function out of a set of transfer functions,
depending on the value of a density function. This sounds quite complicated,
so here is an example: if a density function
and allows for
the selection of a single transfer function out of a set of transfer functions,
depending on the value of a density function. This sounds quite complicated,
so here is an example: if a density function 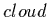 is used to model a cloud,
then perhaps it would be a nice effect to use different emission or scattering
functions for the cloud depending on the density at a point
is used to model a cloud,
then perhaps it would be a nice effect to use different emission or scattering
functions for the cloud depending on the density at a point 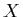 .
MappedTransfer
functions are defined similar to color maps. Given a density function
.
MappedTransfer
functions are defined similar to color maps. Given a density function 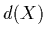 and a number of
and a number of
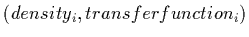 -pairs, the mapped transfer
functions return an interpolated color value:
-pairs, the mapped transfer
functions return an interpolated color value:
or, for in-between values, colors are again linearly interpolated:


Next: Phase Functions
Up: A Flexible Framework
Previous: Density Functions
2000-04-06