Zoltán Konyha
zed@inf.bme.hu
Computer Graphics Group at the Department of Information Technology
Technical University of Budapest
Budapest / Hungary
This paper examines some of the key elements of designing a driving simulation game. We concentrate on graphics and dynamic simulation. The issues of creating and processing the simulation world are addressed. Principles of dynamic simulation are reviewed. Some of the ideas are also applicable to other types of games and real-time graphics applications.
Keywords: computer games, real-time graphics, terrain modelling, particle system, bounding volumes, dynamic simulation, collision detection, collision response.
Up until a few years ago computer games had not been considered an area to benefit greatly from the research in computer graphics and related fields. Since hardware of the price range of desktop computers has become powerful enough to execute recent algorithms real-time, games are quickly becoming one of the financially most beneficial domains of computer graphics.
Parallel to improving visual quality, the illusion of reality is increased by simulating real world physics, too. Driving games are perfect examples where both graphics and physics become important. There are plenty of driving games hitting the market. However, most of them make you drive around fast on a pre-designed circuit to beat your opponents or the clock. Now, we are interested in examining requirements for a game that also lets the player design an outdoor scenario and then drive around, possibly just for the fun of it.
We will first examine possible platforms for the application. In section 3 a virtual world model suited for the application is presented. Section 4 gives a brief review of the dynamic simulator. Section 5 introduces our proposed renderer. Section 6 summarizes directions of possible future development.
The target platform is a middle class home PC equipped with assumably low end graphics hardware. Let us briefly examine the points this implies.
Most home PCs run Microsoft Windows 95/98 or 2000, and we can safely say that these operating systems are currently the primary game platforms. This has been the situation for years now, and it is not likely to change in the near future. Thus the game must run on Windows, however, we also wish to support Linux at least.
It is tempting to create the game as a Java applet which would allow nearly complete platform independence and would lend itself nicely for instant Internet gameplay. Though there are attempts in this field, Java virtual machines are still not powerful enough to handle such an application at interactive rates. Using C++ and keeping Java portability in mind is possibly the best solution for now.
Using graphics hardware acceleration via a library is practically a must for current games. Decision about the graphics library for a game is not very straightforward. For Windows, the combination of Direct3D and DirectDraw are by far the most popular choices. Virtually all accelerators come with Direct3D drivers of some sort. DirectX components do not exist for any other operating systems, though.
The only real alternative is OpenGL [GL], which is in turn supported on a wide variety of platforms. Comparisons of the two libraries demonstrate that surprisingly Direct3D can be a bit faster than GL in games, but this comes at the cost of the Direct3D code being significantly more complicated and cumbersome than the analogous GL code. Sadly, some accelerators do not have GL drivers, which is something we can only hope to change in the future. Anyway, as DirectX is only for Windows variants, opting for OpenGL is evident when we keep portability in mind.
We also have to decide what features of the graphics library we plan to use. When fighting for speed the decision is controversial. Everything that is accelerated by hardware can be expected to work a lot faster through the library. On the other hand, everything that has to be emulated in software is probably faster when done by the application, as it can exploit all the special features of the scene that the library does not know about.
OpenGL has the attractive ability to let the application feed data into almost any stage of the graphics pipeline. Because most current PC graphics cards accelerate rasterization only, that is the only task we plan to be performed via OpenGL. This approach also makes it easier to replace OpenGL with some other library when desired. While graphics libraries are remarkably different in higher layers, they tend to behave very uniformly when it comes to rasterization.
Setting up OpenGL for rasterization is quite straightforward. Both the modelview and the projection matrices are set to identity. Having all the required transformations performed, the resulting 4D homogenous vertex coordinates can be transferred to OpenGL through the usual glVertex() calls or vertex arrays. 4D coordinates are necessary to facilitate perspective correction of texture maps. Lighting is also calculated in the application, so vertex normals do not have to be transferred. To avoid transferring backface polygons to OpenGL, we perform backface culling in the application, too.
State changes such as texture selections are usually expensive. The polygons must be rendered with the smallest number of texture changes. This is easily accomplished if they are first sorted by their texture.
Vertex arrays improve performance by avoiding the overhead of calling functions for each vertex. Best results are generally achieved by using interleaved arrays, but unluckily OpenGL 1.2 does not offer an array format completely suitable for our needs. Separate arrays and glDrawElements() seems to be the most efficient solution.
A typical outdoor scenario consists of the land itself and many static objects such as trees, rocks, buildings, and significantly fewer objects that can move, cars being a trivial example. Additional elements used to simulate natural phenomena that are not intuitively related to real world are particle systems and other special effects.
We want to give the player at least a few square kilometres to freely roam, represent surface features with about 1 metre resolution and keep all this easily editable by the player.
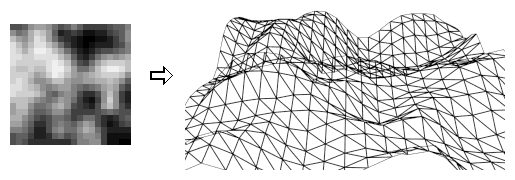
Using parametric surfaces would be sensible, however, we must keep in mind that the player is not an experienced modeller and will easily get confused by control points and surface parameters. A simple height map is more intuitive in the editor, and with 16 bit resolution height values, it requires a moderate amount of memory. The player can edit the map as an image whose colors and shades encode heights. Figure 1 shows the same piece of terrain as height map and rendered as wireframe.

Figure 1: Height map and wireframe render of an example terrain.
Modelling the terrain is made easier by employing fractals and elements of image processing. Rendering 2D random midpoint displacement fractals ('plasma clouds') in the whole image can create a basis for the scenario that can be refined where necessary. We can also add plasma clouds to a portion of the image where we wish to enhance its bumpiness. Rendering midpoint displaced lines helps creating ditches and ridges. For a summary of applying L-systems to create rivers refer to [Mar97]. Some common image processing algorithms were also found useful. Matrix convolution is used for smoothing or enhancing details. Bilinear filtering is not appropriate because of the regular patterns it introduces, bicubic filtering on the other hand proved to create nice maps.
The square defined by 4 neighbouring height map element is a terrain block. Currently each terrain block is assigned to 3 different maps to represent surface features: texture map for rendering the block, bump and drag maps. Height differences and bumps too small to appear in the height map are read from bump maps. The coefficient of friction is similarly read from drag maps. This facilitates easy modeling of mud and puddles. The type of noise from the tyres is another property that may be read from a map.
Moving objects are mesh models designed in modeling software such as 3D Studio Max. However, Max scenes are usually too complex for real-time rendering. Only a limited subset of features can be used and the models are exported in a format that is derived from 3D Studio R4 file format. A single object consists of any number of mesh objects created in 3D Studio.
Moving objects obey the rules of dynamics. When colliding with each other or a static object, they behave conforming to a simple physical model.
Static objects are similar to moving ones, except they are not subjects for dynamics. They may also have keyframe animation, thus they are not entirely static. They are at fixed positions and that is exploited in both rendering and simulation. The potentially visible objects can be identified quickly when rendering. In the simulation module collisions among static objects are never tested, since they have no effect on the objects' possible motion.
When designing the scenario, the player can simply drop the objects where desired.
These are tools to fake natural phenomena that would otherwise be very expensive to calculate. Particle systems add to the realism of the scene when used to simulate smoke, dust, fire or rain. Particles have some basic properties like position and velocity and they are handled uniformly. Importing 3D Studio Max particle systems would be excellent, but it is a challenging task. A simpler system is better suited to real-time application. Additional effects include fog, lens flare and lightning.
The virtual world is preprocessed to facilitate fast collision detection and rendering. The same data structures are used for both tasks to save memory.
Static and moving objects are registered into separate lists and all objects are inserted into an object tree similar to that of Open Inventor [Ment]. Each node contains at least one mesh object and may contain a linear transformation matrix. Two bounding spheres and axis-aligned bounding boxes are created for each object. One sphere and box are tightly fitting the object, the other sphere and box bounds the object and all of its children. Each axis-aligned bounding box (AABB) is defined by the vectors bmin and bmax. They are easily obtained by finding the minima and maxima of the vertex coordinates v along each axis:
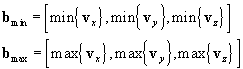 | (3.1) |
Calculating the bounding volumes covering the children is somewhat complicated by the keyframe animation they may have. Both rendering and simulation make use of the resulting combined sphere and AABB tree. Figure 2 shows an example of an object tree.
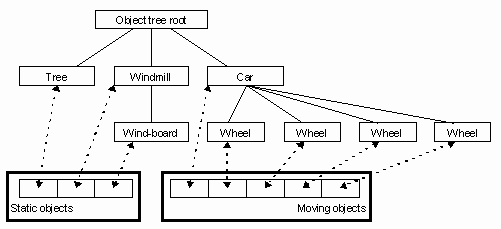
Figure 2: Object tree.
Axis-aligned bounding boxes are created for groups of 2 by 2 terrain blocks. These boxes are recursively grouped 2 by 2 again, creating a quad-tree of bounding boxes. The grid-like nature of the height map makes it possible to avoid the actual pointers. Instead the bounding boxes are entered into an array and the children and the parent of a specific box are easily identified as array indices. AABBs are used because of their memory efficiency. The memory requirement for the whole bounding box structure using single precision arithmetic is moderate at 8n2 bytes for a terrain of n2 blocks.
Furthermore, each static object is projected onto the X/Z plane. The tightest fitting terrain bounding box that covers the projection is located and the object is added to the list of static objects for that bounding box. Figure 3 shows part of a possible terrain grid with objects and the resulting AABB-tree.
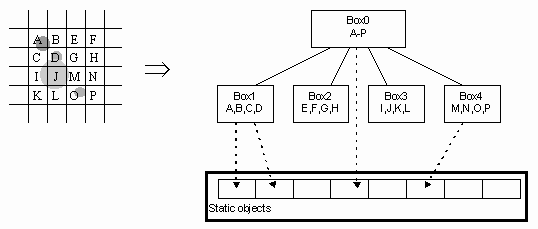
Figure 3: Terrain bounding boxes and static objects. Squares A-P are terrain blocks, circles symbolize static objects.
We are examining a driving simulation, but it is easily pointed out that the core of most 3D games is some sort of a dynamic simulator. The scene comprises objects moving around and interacting with each other and the rest of the virtual world, and we attempt to create a reasonably realistic experience for the player. There are two main approaches for dynamic simulation.
Constraint-based models use non-penetration contact forces to avoid bodies from penetrating each other. Modelling the forces is either accomplished by penalty or analytic methods. Penalty methods [MW88] insert temporary springs that push the colliding bodies apart, though adjusting spring constants practically requires magic. Analytic methods translating non-penetration constrains to linear complementary problem tend to have difficulties when friction is modelled.
Impulse based systems in turn are attractively simple and robust, yet produce realistic results. All contacts between bodies are modelled as collisions. Bodies can travel freely between collisions, possibly influenced by gravity and drag.
Impulse based simulation and related problems are being actively investigated, and for an application where we expect a good number of collisions it seems to be the optimal choice. Hence the simulation consists of three basic tasks: given a system of bodies and forces, dynamically evolve the system for a period of time until a collision happens, then resolve the collision.
The bodies in the system are perfectly rigid, they are not deformed by forces and collisions. Each rigid body has three invariable properties: mass, center of mass and the inertia tensor. The simulator is expected to calculate the position, velocity, orientation and angular velocity of the body resulting from the forces and impulses at collisions.
Position and its time derivative, linear velocity are trivially described by 3D vectors. Specifying 3D orientation is a bit more complicated. Orthogonal 3x3 matrices transform vectors between orthonormal bases and thus provide well-known and trivial representation of orientation. Additionally, quaternion representation is common in keyframe animation because of nice interpolation possibilities. Quaternion algebra is reviewed in [Eb98a], using quaternions in animation is also covered in [SKe95]. Here we provide a brief summary to picture how they can describe orientation.
Quaternions are four-vectors whose elements are usually arranged as a scalar and a three-vector. Quaternions can also be defined as generalization of complex numbers. To express orientation with quaternions we must note that an arbitrary change in orientation can be described by a vector d and the angle of rotation ![]() around d. The quaternion q that performs this rotation is:
around d. The quaternion q that performs this rotation is:
| (4.1) |
Vector u is rotated into v by:
| (4.2) |
The multiplicative inverse of quaternion q is defined as:
| (4.3) |
Orthogonal matrices and quaternions are both non-minimal parametrizations of 3D orientation and have no singularities. However, matrices have 9 parameters and pose obvious redundancy over the 4 quaternion parameters. Non-minimal parametrizations may drift off the manifold and they must be projected back to avoid invalid orientations. Assuring the orthogonality of matrices is somewhat more complex than normalizing a quaternion, so unit quaternions are generally the best choice.
As long as the objects are moving without colliding, they are only influenced by forces like gravity, drag and possible springs. All forces can be summarized as a single force working on the center of mass and similarly all moments can be summarized as a single moment. Until the first collision we can evolve the scene using the Newton-Euler equations (4.4) and (4.5).
| (4.4) |
| (4.5) |
Gravity and drag are modelled as forces applied at the center of mass, thus they do not induce torque. Springs are attached to specific points on the bodies. Having figured out the points where the forces have to be applied, advancing the system is a problem of numerical integration. Integration of orientation with quaternions is covered in [Mir96].
We need to find the first collision in the scene, since the system can be integrated until that point in time. We have to detect collisions between bodies and a body and the terrain, which is a B-spline surface.
Let us consider pairs of objects in the scene. Each object may be moving at a constant velocity and we are interested in whether they collide until the end of the time step, and if they do, when does the collision occur. As described in section 3.5 objects have bounding spheres and bounding boxes.
Detecting object to object collisions exploits the hierarchy information in the object tree. Sparse situations are quickly discovered by testing bounding spheres. Exact collision information is acquired by testing the bounding boxes of objects that are in the vicinity of each other.
An intersection test for moving spheres can be derived by finding the minimum distance of the line segments swept by the spheres as they travel.
Intersection tests for bounding boxes are more challenging. A fast interference algorithm for oriented bounding boxes (OBBs) employing the separating axis theorem is presented in [GLM96]. Enhancement to moving OBBs is introduced in [Eb98b]. An OBB can be defined by its 3 axes and its extents along the axes.
When finding object to object collisions we start at the object trees nodes for the objects involved and simultaneously traverse the tree on two paths. The following pseudocode explains the tests performed. In the pseudocode O1 and O2 are the objects involved, B1 and B2 are the bounding boxes for O1 and O2, S1 and S2 are the bounding spheres for O1 and O2, S1C and S2C are the bounding spheres that include children.
if S1C and S2C collide {
if S1 and S2 collide {
if B1 and B2 collide return "O1 and O2 collide"
}
compare O1 and children of O2 and return if a collision is found
compare O2 and children of O1 and return if a collision is found
compare children of O1 and children of O2 and return if a collision is found
}
return "O1 and O2 do not collide"
Since we typically have few objects moving around, testing each one against all others is an acceptable approach. So the above test is performed for each pair of objects.
The number of static objects is a lot more, however. To avoid testing a moving object against all of them, the moving object's bounding box is projected onto the X/Z plane. Then we find the terrain bounding boxes this projection intersects. The object needs to be tested against the static objects listed in these bounding boxes.
The object's bounding box is tested against the terrain AABB-tree to locate the expected areas of collision. In these areas the terrain is recursively subdivided and an approximate location for the collision is determined.
Collision detection between an object and the terrain does not use the bump map properly. Since the bump map is intended to represent differences in the magnitude of centimetres, this is generally not a problem.
When a collision happens between two rigid bodies, the linear and angular velocities of the objects involved change abruptly. The duration of the collision is infinitesimal. All non-collision forces can be neglected since they have no effect during an infinitesimal period of time. This behaviour is modelled by impulse being applied to the colliding bodies at the point of collision.
To resolve a collision we need one additional piece of information: the collision normal. When at least one face is involved in the collision, the normal is naturally the normal of the face. When two edges of the bounding boxes collide, the normal must be perpendicular to both faces that meet on the colliding edge in both boxes. Thus the collision normal is the cross product of the normals of the faces not sharing the colliding edge. In the case of object to ground collision the collision normal is the normal of the B-spline perturbed by the bump map. This can be derived in a way just like traditional bump maps as in [SKe95].
Approaches for collision response become expensive to compute as they employ the more realistic model of the underlying physics. Except for ideally elastic collisions some of the kinetic energy is dissipated during the collision. This is a result of complex macroscopic and atomic procedures and it is modelled as a single scalar e called coefficient of restitution. Collision time t starts at t=0 and ends at t=tf. The time of the maximum compression t=tmc is the point in time when the velocities change sign. Newton's impact law (4.6) represents the coefficient of restitution as the quotient of the relative normal velocities before and after the collision.
| (4.6) |
Newton's law does not apply to cases when friction during collision is also modelled. In Poisson's theorem (4.7) e equals the quotient of the normal components of the impulse delivered to the body in the compression phase and the restitution phase. This allows for modelling friction, but the total energy of the system can increase unexpectedly.
| (4.7) |
Stronge's hypothesis (4.8) improves by dealing with the work done by the normal components of the collision impulses.
| (4.8) |
An attractive response model based on Stronge's hypothesis is described in [Mir96] where the collision is resolved by integrating the compression and restitution phases separately. Unfortunately, it is a bit complex to evaluate, and for the time being we apply a raw simplification by not considering friction during collision. Therefore we can use Newton's law and calculate collision impulses using simple algebraic functions. Yet this still allows interesting behaviour that generally looks correct enough for a game.
The first step of resolving the collision is calculating the relative contact velocity u from the linear and angular velocities of the objects. Then the collision matrix K is built using the masses and inertia tensors of the objects. The collision impulse p is computed from u and K. Finally the linear and angular velocities of the objects involved are updated based on their masses, inertia tensor and the p. Detailed explanation of the process summarized above is also given in [Mir96].
The scene is rendered in 4 steps: sky, terrain and static objects, moving objects, finally particle systems and other additional effects.
Sky and horizon are rendered using precalculated textures applied to a cube always centered at the camera, similar to the method detailed in [Had98]. Moving clouds can be realized by rendering multiple layers and texture animation. The Z-buffer is neither tested nor updated in this step.
When rendering the terrain and objects, Z-buffer is always tested but only updated for opaque polygons. The terrain is rendered using the bounding box tree described in section 3.5. Starting from the root of the tree the bounding box in the node is tested against the view frustum. If it is trivially accepted, terrain blocks in all of its children can be rendered without any further test. A trivially rejected bounding box terminates the recursion. Children of the bounding boxes intersecting the view frustum must be tested further. The terrain polygons are created on-the-fly. The tesselation can be made adaptive to improve resolution when rendering locations closer to the camera.
At each node visited, the static objects listed are rendered by processing the object tree starting at the node specified by the object. The bounding boxes covering the object's children are recursively tested against the view frustum to allow early culling of any invisible objects. Moving objects are rendered by navigating through their list and processing the object tree starting at the node specified by the object.
Bounding boxes for particle systems are created dynamically based on the particles' maximum velocities and life times and are used to cull the entire system. Rendering particles as single points in OpenGL is not advantageous because points cannot be textured in a useful manner. Also, particles near the camera must be rendered larger, and changing the point size can be costly. Therefore particles are rendered more efficiently as triangles or quads always rotated to force the viewer. This technique is called billboarding and is outlined in [SG98]. The textures for the particles may be animated to allow an additional degree of freedom.
Additional effects include fog, lens flare and lightning. Fog effect is easily achieved with alpha blending. Since real-time rendering of lens flare is out of the question, it is modelled by precalculated and billboarded texture maps. Lightning is simulated by rendering 3D random midpoint displaced lines.
The traditional way of overlaying the cockpit as a bitmap for internal views is rejected in favour of building the car's interior as a polygon model. This makes it possible to look around inside the car and get rid of the unrealistic poster-like appearance.
This paper focused on graphics and simulation issues for a driving simulation game. A virtual world model appropriate for outdoor scenes was reviewed. We investigated use of different bounding volumes for the elements of the virtual world while keeping modest memory requirements in mind. An overview of collision detection and resolution was presented, finally the tasks of the renderer were outlined.
Future work concentrates on both graphics and simulation. Instead of the current AABBs for the objects OBB-trees should be built to allow closer approximation of geometry. In [GLM96] Gottschalk el. al. also present an algorithm for creating an OBB-tree that makes use of the first and second order statistics of the vertex coordinates.
Integrating smooth levels of detail [Sch98] will improve image quality and ease the load on the renderer at the same time. Lights and shadows are still waiting to be implemented.
Calculating friction during collisions would result in much more realistic behaviour, a trade-off between realism and performance must be found. The simulator's integrator should be improved.
We will keep an eye on the performance of Java virtual machines and implement the simulator as a Java applet as soon as it seems to be feasible.
| [Eb98a] | David Eberly: Quaternion Algebra and Calculus, 1998. |
| [Eb98b] | David Eberly: Intersection of Two Moving Oriented Bounding Parallelepipeds, 1998. |
| [GL] | Mark Segal, Kurt Akeley: The OpenGL Graphics System: A Specification (Version 1.2.1), 1998. |
| [GLM96] | S. Gottschalk, M. Lin, D. Manocha: OBB-Tree: A Hierarchical Structure for Rapid Interference Detection, in Proc. of ACM Siggraph'96, 1996. |
| [Had98] | Markus Hadwiger: PARSEC: Enhancing Realism of Real-Time Graphics Through Multiple Layer Rendering and Particle Systems, in Proc. of CESCG'98, 1998. |
| [Mar97] | Ivo Marák: On Synthetic Terrain Erosion Modeling:A Survey, in Proc. of CESCG'97, 1997. |
| [Mir96] | Brian Vincent Mirtich: Impulse-based simulation of Rigid Body Systems, 1996. |
| [Ment] | J. Wernecke: The Inventor Mentor: programming Object-Oriented 3D graphics with Open Inventor, Addison Wesley, 1994. |
| [SS98] | Dieter Schmalstieg, Gernot Schaufler: Smooth Levels of Detail, 1997. |
| [SG98] | Advanced Graphics Programming Techniques Using OpenGL (SIGGRAPH `98 Course), http://www.sgi.com/software/opengl/advanced98/notes/notes.html |
| [SKe95] | László Szirmay-Kalos (editor): Theory of Three Dimensional Computer Graphics, Akadémiai Kiadó, Budapest, 1995. |