Next: Bibliography
Up: paper
Previous: Summary
A further application is sharp image zooming using gradient-based
interpolation. From the original 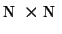 gray-scale image we
want to generate an
gray-scale image we
want to generate an
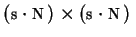 zoomed image.
Using traditional resampling methods, the following problems
arise:
zoomed image.
Using traditional resampling methods, the following problems
arise:
- linear interpolation would result in blurred edges
- nearest neighbor interpolation would cause staircase artifacts
Therefore the goal is to obtain smooth and sharp edges inside a
cell, where the interpolation is performed. The basic idea behind
the gradient based interpolation is, that the original image is
interpolated in each cell on an 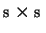 subgrid. At the corner
pixels the gradients are estimated from the original pixels
(central differences or linear regression). The gradients at the
subgrid points are calculated from the gradients of the four
corner pixels using bilinear interpolation. The FFT method is
performed on the entire
subgrid. At the corner
pixels the gradients are estimated from the original pixels
(central differences or linear regression). The gradients at the
subgrid points are calculated from the gradients of the four
corner pixels using bilinear interpolation. The FFT method is
performed on the entire
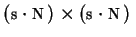 image (the
gradients are known for each pixel and the intermediate pixel
values can be defined as a constant (e.g. the average of the four
corner voxels). In the FFT method relatively high S and G
parameters are used. The penalty function is defined like in the
2D dedithering case [4].
image (the
gradients are known for each pixel and the intermediate pixel
values can be defined as a constant (e.g. the average of the four
corner voxels). In the FFT method relatively high S and G
parameters are used. The penalty function is defined like in the
2D dedithering case [4].
Ivan Viola, Matej Mlejnek
2001-03-22