Parallel Incremental Delaunay Triangulation^[1] 

Josef Kohout besoft@students.zcu.cz
Department of Computer Science and Engineering
University of West Bohemia
Pilsen, Czech Republic

Abstract

We have focused on developing a simple threaded Delaunay triangulation. The algorithm is based on well-known incremental insertion. It works with one shared structure, so there is no need to merge sub-results into the resulting mesh. It was tested on multiprocessors with 2 and 8 processors using up to 8 threads.

Keywords: Delaunay triangulation, parallelization, incremental insertion.

1. Introduction

In many branches of human research, such as scientific data visualisation and interpolation, robotics, pattern recognition or natural sciences, there is a need to triangulate set of points. The popularity of Delaunay triangulation is that the algorithm produces the most equiangular triangles of all possible methods and it can be computed in O(n·log(n)) in the worst case (where n is the number of points to triangulate). However, algorithms with O(n) expected time also exist.
        Due to this popularity, no wonder that construction of the Delaunay triangulation is one of the problems that are tried to be solved in parallel or distributed environment. Parallel version of the Delaunay triangulation based on Divide&Conquer (D&C) method can be found in [1, 4]. D&C looks naturally: problem is recursively divided into two sub-problems that are solved and the resulting triangulation is obtained by merging these solutions. However, there is one important fact: the input set is smaller and smaller at each iteration and therefore processors are unequally loaded. Thank to this fact, the practical results of this approach are usually worse than expected.
        This paper briefly describes two parallel Delaunay triangulation algorithms called pessimistic and optimistic method (details see in [5]). This paper compares both methods and describes possibilities of speed-up (e.g., a use of geometric properties).

2. Incremental Delaunay triangulation

A triangulation T(P) of a set of points P in the Euclidean plane is a set of edges E such that

1. no two edges in E intersect in a point not in P
2. the edges in E divide the convex hull of P into triangles.

Triangulation DT(P) of a set of points P in the plane is a Delaunay triangulation of P if and only if the circumcircle of any triangle of DT(P) does not contain any other point of P in its interior.
        Although incremental insertion algorithm for Delaunay triangulation has O(n²) worst-case and O(n·log(n)) expected-case time complexity, it is very popular due to its simplicity and robustness. The points can arrive on-line and there is no need to know all input points at the beginning because the points are inserted one at a time. However, range of coordinates have to be known in advance. It also allows modification for constrained triangulation [6], for non-Euclidian metrics or for 3D triangulation.
        The algorithm starts with creation of the convex-hull or creation of a temporary large triangle embedding all inserted points. The second possibility seems to be better because the convex-hull construction adds an extra time and one need to differentiate the first level of triangles in the location algorithm. However, using the starting triangles is not without any problem. This temporary triangle must be removed at the end, another problem is also how to choose its vertices. Recommended position in [2] is (K,0), (0,K) and (-K,-K) where K = 3*size of the min-max box.
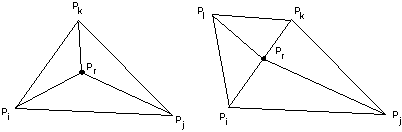
        To insert a point p_r, we must quickly locate the triangle with vertices p_i, p_j and p_k that contains the inserted point. This triangle is subdivided into three new triangles if the point lies inside the triangle (See Figure 1a) or into two new triangles if the point lies on an edge. In the second case also the neighbour is divided as is shown in Figure 1b.

a) Point inside a triangle         b) Point on an edge

Figure 1: Point insertion

        However, after subdivision, some triangles that do not satisfy the empty circumcircle test may exist. In this case the wrong edge between two triangles is flipped. This flip may cause that another triangle does not satisfy the test. The flipping must be applied repeatedly (it is propagated in the waves until all triangles are correct - see example in Figure 2). It means that the insertion of a point may change the whole triangulation.

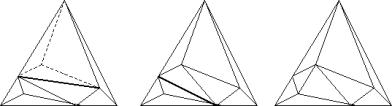
Figure 2:Propagation of flips

        The key problem is how to quickly find the triangle that contains the point. One possibility is to use a directed acyclic graph (DAG) from [2]. DAG is a tree with the history of insertions. Each node corresponds to a triangle; when the triangle is subdivided or flipped, the node gets sons corresponding to newly created triangles. The current valid triangulation is therefore in the leaves and the starting large triangle in the root. Location of the inserted point in this data structure can be done in O(log·n) expected and O(n) worst time. If the order of insertion of the points is randomised, the tree is nearly balanced so the possibility of the worst case is low.
        The algorithm of the randomized incremental Delaunay triangulation is briefly given in Figure 3. For more details see [3] and [2].

procedure Delaunay_triangulation 
Input: A set P = {p_i, i = 0,1,...,n-1} of n points in the plane 
Output: A Delaunay triangulation of P DT(P)

1. begin
2.    Initialize the large triangle;
3.     Compute random permutation of p₀, p₁... p_n-1 of P;
4.     for r:=0 to n-1 do begin // insert p_r  into DT(P)
5.         Locate the triangle p_ip_jp_k Î DT(P) containing p_r;
6.         if p_r lies inside interior of p_ip_jp_k then
7.             Add edges from p_r to the vertices of p_ip_jp_k and subdivide p_ip_jp_k into three triangles;
8.         else // p_r lies on the edge of the p_ip_jp_k , say p_ip_k
9.             Add edges from p_r to p_j and to p₁, the third vertex of the other triangle sharing p_ip_k an subdivide two triangles sharing p_ip_k into four triangles;
10.         Legalize the triangulation; // flipping
11.     end;
12.    Remove all triangles contaning vertices of the large triangle;
13. end

Figure 3: Serial algorithm of Delaunay triangulation by randomized incremental insertion

3. Parallelization

Parallelizing Delaunay triangulation is not easy as each point may influence the whole triangulation. We suppose architecture with several processors and shared memory. Computation will be partitioned among threads. One thread runs usually on one processor. (It is possible to start more than one thread on one processor, but it does not bring substantial improvement). Because each thread works with shared DAG structure, synchronization on them must be implemented. There are three main methods how to synchronize them: batch, pessimistic and optimistic method.

3.1 Batch method

We can modify the serial algorithm as follows. We have several threads that locate in the DAG structure the triangle that contains the input point. Subdivision and legalization are done by one specialized thread that receives input point and input triangle from the searching thread. There is a problem how to ensure communication between the specialized thread and the searching thread. Using queue in shared memory can solve it. If this queue is empty the specialized thread must wait. Question is how long must be the queue to avoid waiting of the searching threads. There is of course the problem that location must take much more time than subdivision and legalization otherwise soon the queue will be full and the performance goes down. Due to these problems we did not implement batch-method of Delaunay triangulation.

3.2 Pessimistic method

The conclusion from measuring the serial algorithm is that the location longs at least 60% of total time needed to construct the Delaunay triangulation (see Figure 4 for details).

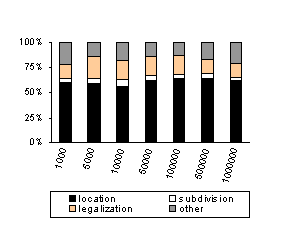
Figure 4: Runtime needed for the main parts of the incremental algorithm for uniform data

Although it might not be enough for the batch method, it is satisfactory for the pessimistic method. Pessimistic method is a modification of the batch method. There is no specialized thread; all threads do the same work. While several threads can read the DAG simultaneously, only one thread can modify it. Threads locate the last parent triangle that contains the input point (reading) then they enter a critical section, finish the location, subdivide and legalize (writing) and finally they leave the critical section.
        Each node in DAG includes a flag categorizing the node as it is shown in the Figure 5. Leaves in the DAG are called children. Regular nodes are such nodes that all their sons are not leaves. The remaining nodes are marked by any combination of L, M and R letters. The letter L means that the first son is leaf - the node is last left parent. The letter M means that the second son is leaf (last middle parent) and finally the letter R means that the third son is leaf (last right parent).
        The location can continue only in regular nodes, e.g. in the MR node we can test the triangle in left son but testing triangles in middle or right sons can be done only in critical section (these triangles are tested only if the input point does not lie in the "left triangle").

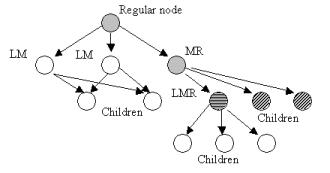
Figure 5: Categorization of the DAG nodes; The letters L, M or R near the nodes means that this node has not grandson in left (L), middle (M) or right (R) direction.

The pessimistic method is simple but it brings limited speed-up due to critical section (see section 5). The algorithm is in the Figure 6. Problem how to distribute work to threads will be discussed later.

Master thread:
Input: A set P = {p_i, i = 0,1,...,n-1} of n points in the plane 
Output: A Delaunay triangulation of P DT(P)

1. begin
2.    Initialize the large triangle;
3.     Compute random permutation of p₀, p₁... p_n-1 of P;
4.     Subdivide P into m subsets where m is the number of threads;
5.     Start all worker threads and wait inactively until finished;
6.     Remove all triangles contaning vertices of the large triangle;
7. end

Worker thread:
Input: A set Pt = {p_i, i = 0,1,...,n_m-1} of n_m points in the plane, Pt Ì P
Output: Modifies the shared DT(P)

1. begin
2.     for r:=0 to n_m-1 do begin // insert p_r  into DT(P)
3.         Start to locate in DAG the triangle on level of leaves' parents containing p_r;
4.         if any thread working with leaves exists then wait;
5.         Enter critical section; // start work with leaves
6.             Finish location on the leaf level and find the triangle p_ip_jp_k Î DT(P) containing p_r;
7.             Subdivision and check of the new triangles;
8.         Leave critical section;
9.     end;
10. end

 Figure 6: Algorithm for pessimistic method

3.3 Optimistic method

Although the flipping may change the whole triangulation, the flipping is obviously done locally. It is not necessary to "lock" all DAG leaves only for one thread. Let all worker threads make location, subdivision and legalization. Of course, we must ensure synchronization among the threads. The location is the same as the location in pessimistic method (it means not protected). In the DAG node, a flag specifying which thread locked the triangle was added. It is required for subdivision and legalization. The worker thread locks all triangles that are accessed and after the input point is inserted, all locked triangles are unlocked. If other thread has already locked the triangle, the thread must wait until the blocking one finishes its work and unlocks this triangle. The algorithm is in Figure 7.
        There exists a possibility of deadlock caused by mutual waiting of threads. This problem can be solved by deadlock detection - the thread which detected the deadlock returns back to the location part and gives up insertion for this moment - or by priorities of threads and by deadlock prevention - the thread is not allowed to wait for a thread with higher priority. Both possibilities (optimistic method with detection and optimistic method with prevention) lead to the use of transactions. Because of low deadlock possibility (see section 5) using the transactions limit the speed-up.
        We can avoid the use of the transactions by a clone of the optimistic method called optimistic burglary method. This method is easy to understand: each triangle in the mesh may be associated with a thing. Each thing (TV set, chair, bed, etc) has its owner - a thread. The things are stored in the house that is owned also by some thread. We assume that all things owned by one thread are in the house owned by the same thread. The plane is so divided into several areas (houses). If a thread modifies triangles that are fully in its house, there is no need to lock the triangles and use transactions. However, sometimes the thread has to enter the house that is owned by its neighbour. Therefore it rings the bell and waits for door opening. The neighbour opens the door when it finished its work and since this time both the guest and host have to lock triangles that are accessed. This solution is not deadlock-safe, because mutual waiting is possible - two or more threads may "ring the bells at the door" without success. We handled this situation by "breaking in": the thread that detects the problem enters and starts its job. When the owner of the house that was attacked, is "awoken", it has to check in each wave of flips whether it is allowed to change the mesh because the burglar could modify non-processed triangles. If the thread is not able to continue in any wave, the counter of potential problems is increased. As we know which triangles were produced when somebody "broke in", we can mark suspicious triangles and correct them at the end of computation. (We did not find more than 5 wrong triangles in any tested data set). The mesh checking adds an extra time and probably that is why the results are worse than our expectations.

Worker thread:
Input: A set Pt = {p_i, i = 0,1,...,n_m-1} of n_m points in the plane, Pt Ì P
Output: Modifies the shared DT(P)

1. begin
2.     for r:=0 to n_m-1 do begin // insert p_r  into DT(P)
3.         Locate in DAG the triangle p_ip_jp_k containing p_r;
4.         while the subdivided triangle or its neighbours are locked by someone other do wait;
5.         Lock the triangle p_ip_jp_k and all its neighbours;
6.         while the legalized triangles or its neighbours are locked by someone other do wait;
7.         Lock the legalized triangles and its neighbours;
8.         Legalization;
9.         Unlock all triangles locked by this thread;
10.         Wake up all threads waiting for this thread;
11.     end;
12. end

Figure 7: Algorithm for optimistic method - deadlock detection

Locking and unlocking of triangles must be done as an atomic operation. It is an easy job if we use the critical section, however, the critical sections, semaphores etc. slow down the computation. Fortunately, it is not necessary to use them, atomic instruction such as XADD, lock INC or lock DEC (Intel x86 instructions) often do.

4. Subdivision of the input points for threads

There are two main principles how to subdivide the input set of points into m subsets that are an input for the worker threads:

1. Input set is statically divided. It means that each thread receives a part of the input set. There is a problem that the last thread gets less than other. However the difference is small in comparison with the size of tasks.
2. Input set is not statically divided but each thread inserts the first not inserted point pointed by a global pointer that is atomically increased. This is called dynamic load.

As it was written previously, it's good to randomise the order of insertion for serial algorithm. However, is it the best for parallel solution? To test this, we implemented also subdivision of the randomised input points according to their geometrical position. Each thread gets the points only from a strip with x-coordinate from the range <x_i,x_i+1> where i is a strip boundary computed by modified algorithm for median^[2] computation that is O(n) in the worst-case, however, in expected-case it has better results. We can also sort the input points according to their x-coordinate, divide them and finally each thread at the beginning of insertion randomise its subset. However, a sort has O(n·log(n)) complexity and therefore it is much slower than the modified median algorithm.

The same can be done for y-coordinate. Or, we "sort" the points according to their distance from the centre (it is x² + y²).

5. Experiments and results

Parallel solution of Delaunay triangulation was implemented in Microsoft Visual C++ v. 6.0 using serial incremental algorithm implemented in Delphi 3. It was tested on Microsoft Windows NT platforms. Tests were run on data sets with n = 5000 up to 500000 and various points distribution (regular grid, uniform or clustered data) on Dell Precision 410 (2x Pentium III, 500 MHz, 1 GB RAM), Hewlett Packard HP XU 6 (2x Pentium Pro, 200 MHz, 128 MB) and Dell Power Edge 8450 (8x Pentium III, cache 2MB, 550 MHz, 2GB RAM). All presented times were obtained as average of 3-5 measuring.

Figure 8 shows the speed-up and the runtime in ms needed to insert all points by the pessimistic method for 2-8 processors and several input data sets. The input set was subdivided into subsets without using the geometric position of them. The distribution was regular grid (it is the most difficult of all distributions according to our tests because the points are close to singular case - more points on the circle - and their insertion leads to many flips; see also Figure 9). These figures show us that the pessimistic method brings limited speed-up for all data distributions. We recommend this solution if someone needs simple parallel Delaunay algorithm up to 4 processors.

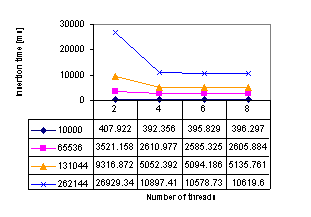
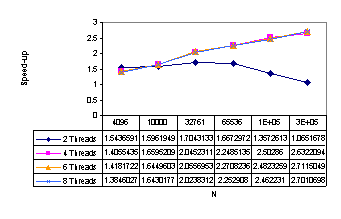
Figure 8: Runtime for different number of points and the speed-up - pessimistic method; tested on Dell Power Edge

        While the optimistic method with deadlock detection needs short code in the critical section, the optimistic method with deadlock prevention makes much more "rollbacks" (i.e., thread must give up the insertion and undo all changes in the DAG that was done by it). The results are almost the same (e.g., n = 65536, detection: 7882, prevention: 7864 ms using 2 threads; n = 500000, detection: 19364, prevention 19724 ms using 8 threads). Therefore only deadlock detection will be presented.

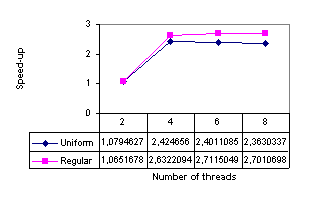
Figure 9: Speed-up for a data set with n = 262144, regular data compared with uniform - pessimistic method; tested on Dell Power Edge

        Figure 10 shows the number of detected deadlocks. This knowledge led us to develop the optimistic burglary method. The number of deadlocks grows up slowly in contrast with the growing input set. For n = 262144 and 8 threads the deadlock must be solved only 143 times while 262001 points are inserted without any problem (it means one problem in 2000 cases).

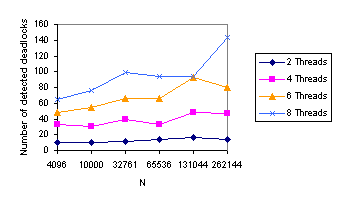
Figure 10: Number of deadlocks

        Figure 11 presents the results obtained by the optimistic method with deadlock detection and optimistic-burglary method. We recommend this method for all input data sets for multiprocessors with 4 or more processors. Although the optimistic burglary method reaches higher speed-up (5.8 for 8 PEs), this speed-up is not adequate to the method complexity and it has even some anomaly for 2 PEs. Thatĺs why we fully recommend the optimistic method with deadlock detection (speed-up 5.7) that has also good results for multiprocessors with 2 PEs.
        We also tested influence of the subdivision according to the geometric position of the points. To do that we modified the algorithm for median computation. This algorithm is faster than a standard sort algorithm - see Table 1.
        We were surprised that the influence of the subdivision according to the geometric position of the points isn't too important - see Table 2 for details. The importance grows with the increasing number of threads and number of input points. The speed-up is about 8% for n = 131044, however, the presented times do not include the time needed for "medians" computation. If it is included, the speed-up is only 4% for the same data set. For some combination of number of threads and number of points the speed-up may be negative. In the optimistic method with deadlock detection is the situation with the dependence of the speed-up on subdivision method worse. There is no speed-up for any input data set tested by using 2 threads (-11% for data set mentioned previously). For this data set, the speed-up is only 0.2% for 4 threads and -0.2% for 8 threads. Similar results we obtained for the optimistic burglary method: -4% in average.

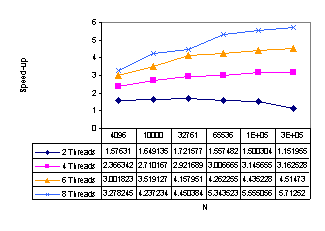
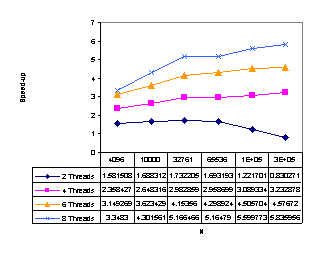
a) deadlock detection                                         b) burglary method
Figure 11: Speed-up for optimistic methods

^* The input set was split into two subsets; the measuring was 3x repeated. All times are in ms.

Table 1: The comparison of division by median vs. sort; Intel Celeron 533Mhz, 256MB RAM

Table 2: The comparison of the subdivision methods; N is number of points, S_x simple subdivision, X_x subdivision according to the x-coordinate and XY_x is subdivision according to both coordinates; It was tested by using 2, 4, 6 and 8 threads, all times are in ms.

        In addition we tested several real data sets. One of them is shown in Figure 12. This data set has 41853 points and the speed-up was 1.71 by the optimistic method with deadlock detection on multiprocessor with 2 PEs ľ Dell Precision 410.

Figure 12: The Delaunay triangulation of a real data set

6. Conclusions

We suggested and tested several methods how to parallelize the serial algorithm of Delaunay triangulation that were called pessimistic, optimistic-detection and optimistic-burglary. The pessimistic method is very simple, however, it is useless for workstations with more than 4 processors. The optimistic-detection method shows relatively good speed-up (up to 5.7 for 8 processors) but the implementation is more difficult. The optimistic-burglary shows even better speed-up (up to 5.8 for 8 processors) but it has an anomaly for workstations with 2 processors where the speed-up may be even worse than one.

7. References

[1] Blelloch, G.E., Miller, G.L., Talmor, D.: Developing a Practical projection-Based Parallel Delaunay algorithm, Proc of the 12^th Annual Symposium on Comput. Geometry, ACM, 1996

[2] de Berg, M., van Kreveld, M., Overmars, M., Schwarzkopf, O.: Computational Geometry. Algorithms and Applications, Springer-Verlag Berlin Heidelberg, 1997

[3] Guibas, L.J., Knuth, D.E., Sharir, M.: Randomized Incremental Construction of Delaunay and Voronoi Diagrams. Algorithmica (7), pp. 381-413, 1992

[4] Hardwick, J.C.: Implementation and Evaluation of an Efficient Parallel Delaunay Triangulation Algorithm, 9^th Annual Symposium on Parallel Algorithm and Architectures, pp. 22-25, 1997

[5] Kolingerová, I., Kohout, J.: Pessimistic Threaded Delaunay Triangulation, GraphiCon'2000, pp. 76-83, 2000

[6] Vigo, M.: An Improved Incremental Algorithm for Constructing Restricted Delaunay Triangulations, Computers & Graphics 21, pp. 215-223, 1997