The finite element mesh

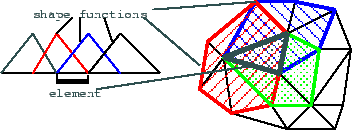
In order to understand what the finite element mesh is, we have to have a look at the shape functions and the direct meaning of computational values. The construction of the approximate solution can also be considered an interpolation, where the variables represent values at given points of the space, and the shape functions are the weighting functions. In this aspect, every variable has a point associated to it at the maximum of the weighting function, called a node in the finite element mesh. During the calculation, it is crucial to identify the nodes the values of which contribute to the value at a given point. The set of points that share the same influent nodes is called an element. Using the usual linear shape functions, elements will be convex polyhedra with nodes at the finite element nodes. Finding the most appropriate nodes and elements, the process called mesh generation, actually means selection of the shape functions. Therefore, it influences the composition of the approximate solution and thus, the accuracy of the computation[3].

Figure 2: Shape functions and elements in one and two dimensions

A mesh is composed of non-overlapping elements that cover all of the examined space without holes. Because the shape functions should be as symmetrical as possible, the touching elements should not have significantly different size or shape. However, as the computation is more accurate where the elements are smaller, it should be possible to locally control the accuracy via a gradual change in element size. It is also important that the elements fit the bounding surface, or the surfaces separating homogeneous volumes, because elements are treated as a unit in the calculations and handling inhomogeneous elements is therefore complicated. It is difficult to meet all these requirements with a regular mesh in which the connections between nodes and elements follow some simple rule. As there is no advantage taken of mesh structure in the finite element method, irregular meshes are generally used. Generation algorithms either aim to create a hexahedral element mesh easy to comprehend, or make use of the flexibility of Delaunay meshes composed solely of tetrahedra. Generally, what we are left to work with after the solution of the equations is a mesh of nodes and elements, with known connections, and time series of various data associated with the nodes or the elements. Some of them are scalar values like saturation or concentration, but there also are vectors like flow velocities. Moreover, values calculated at discrete nodes are related to the approximate continuous solution we may also wish to display. Further on in this paper, we will make use of that structure to visualise the results.