Topological techniques for shape understanding

Silvia Biasotti
silvia@ima.ge.cnr.it

Istituto per la Matematica Applicata
Consiglio Nazionale delle Ricerche
Genova / Italy

Abstract

This paper presents our recent results in the field of surface representation based on topological coding. In particular, we investigate a possible way to adapt to discrete surface models some theoretical concepts as Morse theory and Reeb graphs which bases on differential topology. Starting from a triangulated surface, our aim is to code the relationship among critical points of the height function associated to the mesh. We named Extended Reeb Graph (ERG) the graph representation which can handle also degenerate critical points. The ERG gives an effective representation of the surface shape available for classification, simplification and restoring purposes.
 

KEYWORDS: shape graph, discrete critical point analysis.

1  Introduction

Geometric modelling deals with the representation and manipulation of geometric objects in a computer and it includes the theoretical and application areas of computer science that deal with geometry, such as computer graphics and animation, computer-aided design, discrete computational geometry, etc.. All development in geometric modelling has focused on geometry, which provides a complete description of the (geometric) shape of a solid. The choice of a mathematical model is mainly determined by a set of restrictive computational requirements such as representational finiteness, constructivity and completeness, which are related to the properties of the mathematical model. Nevertheless, there is a clear evidence that shape information is somehow treated differently by the human brain than other forms of information. Even if remaining in the world of geometry, indeed, we use different levels of mental models for describing geometric objects, which provide both high (specific) and low (generic) level shape descriptions [1]. The common characteristics of the mental models is that they all generally refer to shape or function, that is, they are different ways of answering questions such as "What does it look like?", "What is its meaning?". This suggests a shift in the focus of modelling from the detailed specification of bunches of geometric primitives to description of shapes and tools to handle these descriptions.

Topology as the study of shape properties that do not change under deformation, gives a formal framework for the formalisation and solution of several problems related to shape and shape understanding. From this point of view, it is interesting to investigate the possible role of the new field of computational topology, firstly introduced in [2] and followed by [3,], for incorporating abstraction mechanisms in shape modelling.

Shape abstraction tools are necessary to catch the uniqueness properties which identify shapes independently of their particular geometry because similar shapes may occur in a variety of geometrical instances. Differential topology and geometry have been often used for surface coding: tools such as the Euler's equation, surface networks, Morse theory or the Reeb are examples of techniques and measures with an extremely high abstraction power. Applications of these tools have been studied by Nackmann, Pfaltz, Shinagawa, Kunii [5,,].

In this paper we present the description of an high-level abstraction model for the representation and the manipulation of three-dimensional surfaces. Such a model adapts and extends to the discrete domain the basic concepts related to Reeb graphs. Then the resulting representation guarantees the computational efficiency and an effective topological coding of the object allowing a qualitative quick comparison among objects. Research on the use of such a graph for terrain representation has been presented in [8,9] aimed at the definition of innovative, effective and efficient algorithms for understanding, compression and restoration purposes. The proposed extension does not distort the semantic meaning of the Reeb graph and faithfully represent the surface morphology [10]. Moreover the proposed model has been successfully extended to three dimensional closed surfaces represented by triangulation [11].

The reminder of this paper is organised as follows: first, we present some approaches to differential topology, critical points and topological graphs in the computer graphics community; then, basic results of Morse theory and Reeb graph are introduced. In section 4 the ERG representation and some examples of its application are given; in the final section conclusion and future work are drawn.

2  Previous work

Morse theory allows coding the topological relationship among critical points and describing differentiable manifolds using a limited number of information [12]. Generally the knowledge of the critical point configuration is considerated as one of the simplest way to describe the perception and the oraganization of the surface shape, [13]. Many applications of the critical point definition and Morse theory have been proposed in computer grahics to represent implicit surfaces [3], polygonal meshes [4] and discrete solids and surfaces modelling [7,14]. In particular in [4] the authors investigated on the extraction of a Morse function of the surface based on the expansion of a wave transform. An analogous criterium of expansion on polyedral surfaces is the wavefront propagation applied by Wood et al. [15] to coarse mesh extraction. In particular, this method codify and eliminate the region of the surface where the topology does not change.

The main difficulty in the application of topology-based tools is the necessity of adapting concepts developed for smooth manifold to surface models which are only continuos as in the case of triangulated surfaces. Several authors have underlined the importance of these tools in different applications: under the assumption that critical points are non-degenerate, Nackman, [5], proposed an interesting method for coding the critical points of smooth Morse functions of two variables in a Critical Point Graph (CPG). For geographical applications Pfaltz studied a similar approach for discrete surfaces defining the so-called surface networks, [6]. Surface network, moreover, have bee, used by Bajaj, [16] for driving the simplification of meshes while preserving the topology of the shape. Falcidieno and Spagnuolo, [17], defined a curvature-based graph corresponding to a subdivision of the surface in simpler shaped sub-regions.

Major research on the use of topology for surface description has been proposed by Kunii, Shinagawa et al., [7,14], where a surface coding based on Morse theory and Reeb graphs has been defined. Such a kind of model describes a manifold surface by considering the evolution of the surface sections; in practice this model is particular efficient to evidence the topological structure of the surface and to allow a better quote recognition. The resulting conceptual sketch simplifies the topological analysis, it is based on only few elements and it can be associated to reconstruction or generation rules which allow to restoring the original surface. Another method to reconstruct surfaces from contours has been defined from Giertsen et al., [18]; the topological information of this structure can be more efficiently expressed by the Reeb graph, which allows to univocally code contour connectivity and adjacency relationship among sections. Moreover, starting from the notion of Reeb graph in [8] we proposed a topological structure, called ERG, available for surface simplification and reconstruction (for details on the ERG see section 4).

3  Theoretical background

The mathematical basis of the theories here considered concern with topology, in particular differential topology. The idea behind the study of topology is the analysis of the properties of a shape that do not change under deformations [12,3]. In particular any deformation is allowed so long as it is ono-to-one and bicontinuous, which is sufficient to prevent the deformation from cutting segments and piercing holes. In computer graphics the topology is useful both in topological interrogation and in topological control of the models and is called computational topology. Often, in surface modelling, the topology and the algebraic topology have been source for powerful shape abstraction tools as the Euler's equation, the Betti numbers, the surface networks, the Morse Theory and the Reeb graphs.

3.1  Morse theory

Morse theory relates to the study of the relationships between a function's critical points and the topology of its domain, [12]. That theory allows describing differentiable manifolds using a limited number of information, for example by coding the topological relationship between the critical points, [12,19]. Morse theory not only indicates when the topological type changes but what kind of change occurs and it is a fundamental tool in the topological analysis of surfaces (2-manifolds).

Formally, let f be a real function defined on a manifold M and p = p(x, y, z) a point of M; then the relationship grad(f(p)) = 0 defines a critical point of the function f.

The topological type of the immersed portion of the manifold changes after the critical points are dunked. To define the topological type of a critical point we require it is non-degenerate, that is the Hessian matrix of f is non-singular at that point (the Hessian matrix is the matrix of the partial second derivatives of the function f). In particular a function f is called Morse if all its critical points are non-degenerate.

An intuitively good function to study the surface shape is the height function, that is the real function which associates to each point on the surface its elevation. If the function f is Morse the type of the topological changes on the surface are determined by the type of the critical points, which is given by the number of negative eigenvalues of its Hessian. According to the number of negative eigenvalues of the Hessian the non-degenerate critical points of a surface define the 0, 1, 2-cells. In this way it is possible to extract a topological graph based on points, edges and faces called in algebraic topology as the CW-complex, [12]. An important result of Morse theory, which establishes a link between the number of critical points and the topological type of the manifold, is given by the Euler formula: # minima - # saddles + # maxima = 2(1-g) = c(M) where g represents the genus of the surface. In particular, the entity c(M) is called Euler characteristic of the manifold M.

3.2  Reeb graph

In 1946 Reeb proposed considering a topological graph defined as quotient space of a manifold which, under opportune hypotheses, defines the skeleton of the manifold itself, [20]. Considering, for example, the height function f associated to a manifold M = M(x, y, z), the Reeb graph is the quotient space given by the relationship which identifies the points x1 and x2 having same function values and belonging to the same connected component of the inverse image of f. Formally:

Let f:M ® R be a real valued function on a compact manifold M. The Reeb graph of M wrt f is the quotient space of MxR defined by the relation ÔÔ @ ÕÕ, given by:

(x1, f(x1)) @ (x2, f(x2)) Û f(x1) = f(x2)
and x1 and x2 are in the same connected component of f-1(f(x2)).

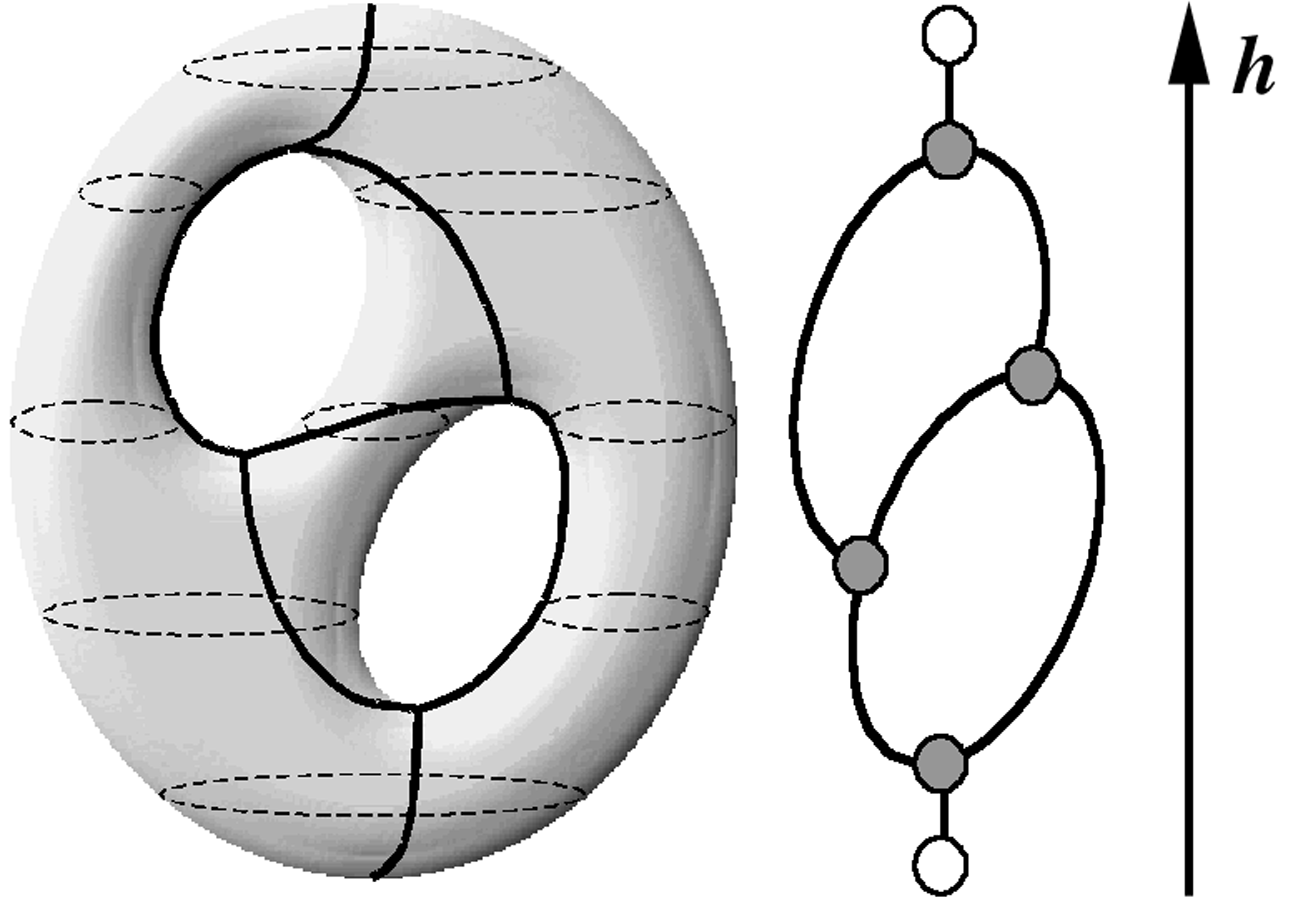
The Reeb graph is a CPG graph: in fact the Morse theory guarantees that the surface topology changes only in correspondence of critical points, that is in the graph representation the nodes correspond to critical points and the arcs are given by the part of surface between two critical levels. Moreover, under the assumption that the height function is Morse, the structure of the Reeb graph is rather simple and represents the topological skeleton of the object. For its properties the Reeb graph ensure an efficient topological control in the compression and simplification problems. In figure 1 the Reeb graph of a bi-torus is shown, in this image the mapping function is the natural height function.

Figure 1: The Reeb graph of a bitorus and some cross sections. Each contour determines an equivalence class which is represented in the Reeb graph by a single point.

4  ERG representation

The straightforward application of the Reeb graph definition to a generic polyhedral surface (e.g. a 3D triangulated manifold) requires at first the definition and the extraction of the critical points, for a detailed definition of critical points for triangular meshes see [16,21,22].

The possible definitions of discrete critical points, however, generally suffer of instability in the sense that small perturbations of the vertex coordinates may result in rather different configurations [23,]. Regarding that, it is necessary to adapt the traditional surface shape classification to polyedral surfaces extending, where it is possible, the usual definition of critical point. This is a well known problem in the computer graphics community but it was not univocally resolved yet. Our proposal is to describe a topological graph, we called Extended Reeb Graph (ERG). Such a graph derives from the direct application of the Reeb graph to degenerate as well as non-simple height functions and keeps the same meaningful properties. The extension proposed relates also the critical area definition and it is coherent with the common idea of critical point. In this manner the analysis of complex handmade articles is allowed even if characterised from multiple flat areas.

The ERG representation for 2.5D surfaces represented by triangular meshes, for example digital terrains, has been fully described in [10,23], and an extension of the method to closed three-dimensional surfaces (i.e. without boundary) has been introduces in [11].

The innovation of our method is both the way of constructing the graph and the efficiency in dealing with degenerate situations. The proposed approach is actually not an extension of the Reeb graph itself, but rather a full application of its definition in the discrete domain, which does not require the height function to be Morse. The main idea is to consider critical areas instead of critical points and identify, starting from them, the smallest area on the mesh whose behaviour is topologically equivalent to the critical area (influence zone). Starting from a triangulated surface constrained to the contour levels generally critical areas are localized by flat regions. The classification of critical areas as maxima, minima and saddles is done by checking the number of non-constrained edges in the boundary and analysing the ascending/descending direction of the surface across the boundary, (for details in the classification see [10]). Since we do not require the height function to be Morse we admit multiply-critical areas as volcano rims. Multiply-connected critical areas divide the surface in an external and, at least, an internal part and are further classified as complex minima, maxima and saddles respectively. In particular, our definition of critical areas still satisfied an extended version of the Euler formula presented in 3.1, for details see [9].

The concept of critical area is not able to fully describe the topologicl behaviour of the surface around saddles, so we have introduced the notion of influence zone of a critical area (see [10,11,23]). Influence zones are the starting points to identify the portion of the mesh which defines the arcs of the ERG and are defined as the smallest areas of the surface having the same topological behaviour as the critical areas (the extended definition of influence zone can be found in [11]). In particular the influence zone of a saddle area is composed by the whole part of the surface contained in the nearest contours (generally at least 3) to the critical area itself. In figure 2(a) we depict the critical areas of a bi-torus while in 2(b) the influence zones are shown, in particular the influence zones of saddle areas detect the region of the triangulation where the topology changes.





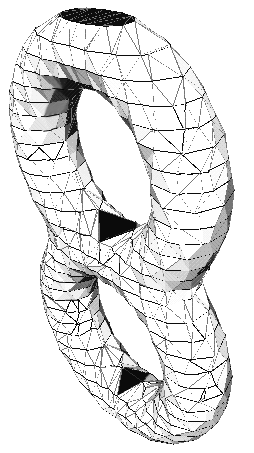
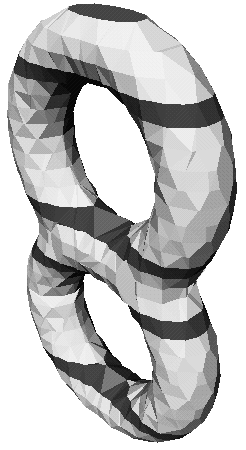
Figure 2: The critical areas (a) and the influence zones (b) of a triangulated bi-torus.

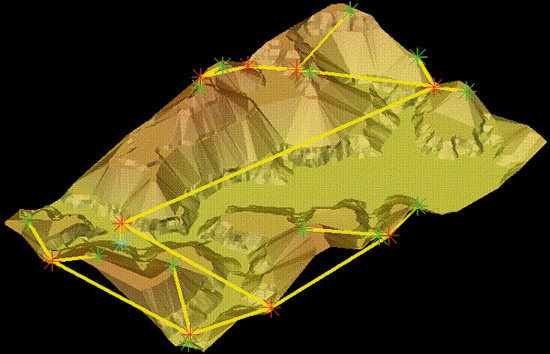
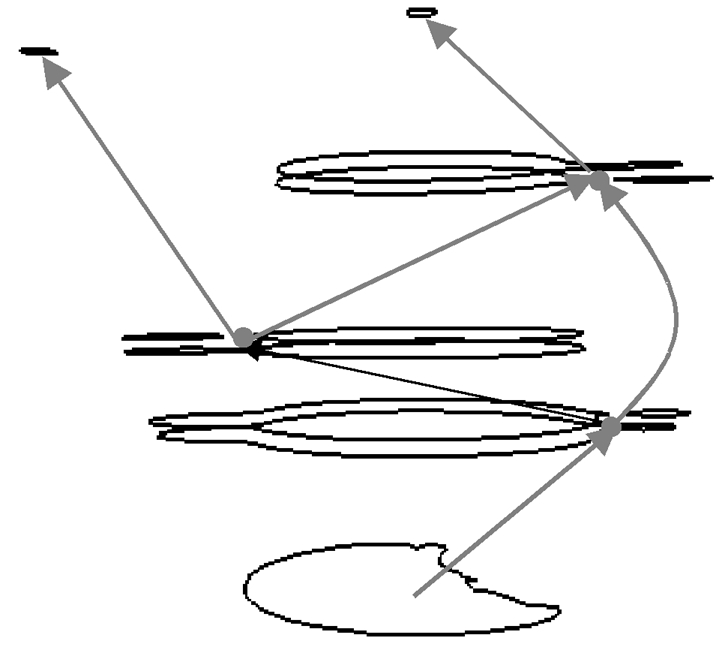
The components of the ERG are defined as follows: nodes correspond to the influence zones of simple critical areas and macro-nodes are used to represent complex critical areas. Finally, the ERG arcs encode the topological adjacency among influence zones and are detected using an expanding process as described in [11]. In figure 3 an example of the ERG extraction for a natural surface and the simplified model built considering only the critical sections are shown. In figure 4 we show the ERG represention of a three-dimensional object: a tea-pot, in particular in 4(a) the influence zone of the critical areas are highlighted.

(a) (b)

Figure 3: The ERG representation of a real surface (a) and the simplified triangulation: the topology of the two models is the same.

(a) (b)

Figure 4: The influence zones of a tea pot and its ERG, (a): in (b) the relations among the critical sections are depicted

5  Conclusions and future work

The structure of the surface is detected by considering the evolution of the surface sections and it is usable for simplification, compression, animation and manipulation purposes. The ERG structure, however, it is insufficient for surface reconstruction purposes: the reconstruction process, in fact, needs major information about the connection of two adjacent sections. It is necessary not only know the adjacency between the sections but detect "how" the tiling should be done and "which" points have to be connected. To do that, could be useful to study each section' shape and to establish the way in which each shape converts into another in terms of similarity. In order to detect the shape similarity among contours it seems opportune to consider the skeleton schematisation of the external shape. In this context the skeleton is a reduction of a shape to its minimal form and it can be considered as a linear approximation of the Medial Axis Transformation (MAT). In particular the MAT of a polygon is the set of centres of the inscribed circles at least bi-tangent to the polygon edges (for a detailed MAT definition see [24]). The high computational complexity of the MAT detection algorithm justifies the choice of a MAT approximation; in this way it is possible to obtain an efficient descriptive power (see [25,]). Then our task is the definition of a complex structure more complete thant the ERG does, which codes the topological skeleton of the object and, in order to favourite the reconstruction process, for each section preserves the basic skeletal information.

Another possible application of the proposed model could be the study of the metamorphosis (morphing) of objects. This application field needs a model that gets out a rapid topological detection, classifies the common shape features and preserves the low-level geometrical information. Such a representation has to allow the transformation and modification directly on the model and give an effective theoretical support. In fact, morphing is a technique used for the evolution and metamorphosis analysis from one image to another. The idea is to get a sequence of intermediate configurations which when put together with the original surface would represent the change from one to the other. This technique has been developed for study both the object evolution (for instance to analyse a sequence of face expressions) and the transformation between different entities. One of the most time consuming tasks in morphing is selecting the points or lines in the initial and final image so that the metamorphosis is smooth and natural and it is not trivial problem to identify which edge should be mapped to which other edge (for details see [27,26]). The interpolation between two shapes can produce forms covering a variety of topological types, that is the topology of intermediate models can be different from the original ones. To investigate the maintenance of the topology when performing a shape transformation shape recognition tools are essential and in this context our representation model could be useful both in shape recognition and in evolution metamorphosis process.

Acknowledgements

Thanks are given to Dr. Bianca Falcidieno and Dr. Michela Spagnuolo for their precious support on the development of the work here presented, and to the whole Computer Graphics group at the IMA-CNR for the helpful suggestions and the technical support.

References

[1]
Falcidieno, B., Spagnuolo, M.: Shape Abstraction Paradigm for Modelling Geometry and Semantics, in Proc. of Computer Graphics International, pp. 646-656, Hannover, June 1998.
[2]
Dey, T. K., Edelsbrunner, H., Guha, S.: Computational Topology, in Advances in Discrete and Computational Geometry, eds: Chazelle, B., Goodman, J. E.; Pollach, R., Contemporary Mathematics 233, AMS, Providence, pp. 109-143, 1999.
[3]
Hart, J. C.: Computational Topology for Shape Modeling, in Proc. of Shape Modeling International `99, pp. Aizu-Wakamatsu, Japan, March, 1999.
[4]
Axen, U., Edelsbrunner, H.: Auditory morse analysis of triangulated manifolds, in Mathematical Visualization, H.-C. Hege, and K. Polthier eds., pp. 223-236. Springer-Verlag, Heidelberg, 1998.
[5]
Nackman, L. R., Two-dimensional Critical Point Configuration Graphs, in IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. PAMI-6, No. 4, pp. 442-450, 1984.
[6]
Pfaltz, J. L.: Surface Networks, in Geographical Analysis, Vol. 8, pp. 77-93, 1990.
[7]
Shinagawa, Y., Kunii, T. L., Kergosien, Y. L.: Surface Coding Based on Morse Theory, in IEEE Computer Graphics & Applications, pp. 66-78, September 1991.
[8]
Biasotti, S., Mortara, M., Spagnuolo, M.: Surface Compression and Reconstruction using Reeb graphs and Shape Analysis, in Proc. of Spring Conference on Computer Graphics, pp. 175-184, Bratislava, May 2000.
[9]
Biasotti, S., Falcidieno, B., Spagnuolo, M.: Shape Abstraction Using Computational Topology Techniques, in Proc. of the Seventh Workshop GEO-7 organized by the IFIP Working Group 5.2, Parma, 2000.
[10]
Biasotti, S., Falcidieno, B., Spagnuolo, M.: Extended Reeb Graphs for Surface Understanding and Description, in Proc. of 9th Discrete Geometry for Computer Imagery Conference, LNCS, Springer Verlag, pp. 185-197, Uppsala, 2000.
[11]
Attene, M., Biasotti, S., Spagnuolo, M.: Remeshing Techniques for Topological Analysis, to appear in Proc. of Shape Modelling International 2001, Genova, Italy, 2001.
[12]
Milnor, J.: Morse Theory, Princeton University Press, New Jersey, 1963.
[13]
Pentland, P.: Perceptual organization and representation of natural form, in Artificial Intelligence, Vol.28, pp. 293-331, 1986.
[14]
Shinagawa, Y., Kunii, T. L.: Constructing a Reeb graph automatically from cross sections, IEEE Computer Graphics and Applications, 11(6), pp 44-51, 1991.
[15]
Breen, D., Desbrun, M., Schröder, P., Wood, Z.: Semi-Regular Mesh Extraction From Volumes, in Proc. of IEEE Visualization 2000, pp. 275-282, 2000.
[16]
Bajaj, C., Schikore, D. R.: Topology preserving data simplification with error bounds. in Computer & Graphics, Vol. 22, No. 1, pp. 3-12, 1998.
[17]
Falcidieno, B., Spagnuolo, M.: A new method for the characterization of topographic surfaces, International Journal of Geographical Information Systems, Vol. 5, No. 4, 1991.
[18]
Giertsen, C., Halvorsen, A., Flood, P. R.: Graph-directed modelling from serial sections, The Visual Computer, 6(5): 284-290, 1990.
[19]
Guillemin, V., Pollack, A.: Differential Topology, Englewood Cliffs, NJ: Prentice-Hall, 1974.
[20]
Reeb, G.: Sur les points singuliers d'une forme de Pfaff completement integrable ou d'une fonction numérique. in Comptes Rendus Acad. Sciences, Vol. 222, pp. 847-849, Paris, 1946.
[21]
Banchoff, T.: Critical Points and curvature for embedded polyhedral surfaces, American Mathematical Monthly, Vol. 77, pp. 475-485, 1970.
[22]
Takahashi, S;, Ikeda, T., Shinagawa, Y., Kunii, T. L., Ueda, M.: Algorithms for Extracting Correct Critical Points and Construction Topological Graphs from Discrete geographical Elevation Data, in Proc. of Eurographics '95, Vol. 14, Number 3, 1995.
[23]
Biasotti, S.: Rappresentazione di superfici naturali mediante grafi di Reeb, Thesis for the Laurea Degree, Department of Mathematics, University of Genova, September 1998.
[24]
Blum, H.: A transformation for extracting new descriptors of shape, In Proc. Symp. Models for Perception of Spheech and Visual form, Whaten-Dunn, W., Ed. Cambridge, MA: MIT Press, pp. 362-380, 1967.
[25]
Lee, D. T.: Medial Axis Transform of a Planar Shape, in IEEE Trans. Pattern Analysis and Machine Intelligence, Vol. PAMI-4, pp. 363-369, July, 1982.
[26]
Mortara, M., Spagnuolo, M.: Similarity Measures for Blending Polygonal Shapes, in Computer & Graphics, Vol. 25, No. 1, 2001.
[27]
Alexa, M.: Merging Polyhedral Shapes with Scattered Features, The Visual Computer, 16, 1, pp. 38-46, 2000.
File translated from TEX by TTH, version 2.25.
On 22 Mar 2001, 12:15.