We have implemented efficient algorithms for view frustum culling introduced in the article Optimized View Frustum Culling Algorithms for Bounding Boxes [1] by Ulf Assarson and Thomas Möller (2000). We measure and evaluate the efficiency of selected speed-up techniques used in static and dynamic scenes.
Keywords: view frustum culling, bounding volumes, scene hierarchy.
We have examined the article Optimized View Frustum Culling Algorithms for Bounding Boxes [1] and also the following technical report by the same authors Optimized View Frustum Culling Algorithms [5] which presents generalized and detailed parts of the basic article.
In this section we will describe briefly the main novel ideas of optimization methods that Assarson and Möller introduced in [1]. The following explanation is also used as the basic information about our implementation of the presented methods. We will also include a detailed description, critical comments and remarks about changes in our implementation. The presentation of the abilities of our application will take place in Section 3 including the discussion about the results in Section 4 and 5.
Moreover the general methods the authors of [1] present also speed-up techniques which use low degree of freedom of the camera motion in the user-driven walk-through the scene. This is significant for well known 3D computer games driven by a player from his own point of view.
All methods are independent each other. It is possible to determine stand-alone success in comparison with another VFC algorithms. Möller et al. used the VFC algorithms of DirectMode (DirectModel 1.0 Specification, Hewlett Packard) and Cosmo3D (Cosmo3D programmers' guide, Silicon Graphics Inc.) as a measure ethalon for establishing presented speed-ups.
All measurements were performed for several types of bounding volumes and their hierarchy in scenes consisting of about 150 thousands of polygons. They provide a solution which is 3-10 times faster than DirectModel a system that uses the axes aligned bounding boxes hierarchy, and 1.2-1.4 times faster than Cosmo3D with the hierarchy of bounding spheres.
The visible volume of the camera is represented by six planes. Two of them (near and far) are parallel. The other four are connected in one point of space that represents the viewpoint. They inclined a spatial angle that represents the FOV field of view of camera. The far plane bounds visibility of far objects in space. The near plane determines the distance of the view-port from the viewpoint.
Möller et al. specify the VF (viewing frustum) as an axes symmetrical quadrilateral frustum. Often the reduced versions of the viewing frustum without the far plane and sometimes without the near plane are used in practice. The near plane of VF could be changed to the spherical surface in cases when we need to render objects in a panoramatic projection.
The most commonly used bounding volumes for the VFC are already mentioned AABBs and spheres, but also the OBB (oriented bounding box) or the k-DOP (discrete oriented polytope) [7]. The volume of the object in proportion to the volume of its bounding solid determines the conservativity of the elimination algorithm. The closer are the volumes the harder is the implementation of such a VFC algorithm. The VFC algorithm based on bounding spheres is simple and fast. That is the reason for no really significant speed-up improvements as is shown on the results in [1].
The most commonly used structure that is good compromise between the tight-fitting k-DOPs and conservative spheres is the AABB. The important property of the AABB is aligning to the world coordinates. In contrast to the OBB, that is transformed by the same matrix as the vertices of the bounded volume, many transformations can be removed in the case of AABB. Still there is need to transform the AABB if the object rotates. Good compromise for this case can be a combined hierarchy of the bounding boxes. There are the OBBs in leafs of the oriented acyclic graph of the scene, from which the AABBs on the higher levels of the hierarchy can be easily computed only by a transformation and by finding the bounds of the eight vertices set.
Clark [2] shown that the scene hierarchy is really important data structure that helps speeding up the VFC significantly. Möller et al. obtain the best results for speeding up the eliminating phase with the hierarchy of the AABB. The more complex hierarchy with the k-DOP elements was not used by the authors, but most of the optimization ideas can be used even for these complex structures.
There should be noted that the authors did not describe the way how the AABB hierarchy was created, its implementation, how and how often they refreshed the dimensions of the bounding volumes, whether the scenes consisted of some animated solids etc.

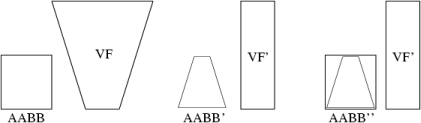
The entire procedure is in Figure 1. The AABB and the VF is transformed by the perspective transformation that reduces the VF to a box. This transformation needs 72 multiplications. The new AABB is constructed around the original VF. The collision detector is applied on this couple and can be realized by the six comparisons.
An important feature of the basic algorithm is its conservativity in the sense of the detection of the state where the bounding volume intersects the visibility volume of the camera. Low precision of this test can cause unnecessary culling of a big amount of triangles of an object inside the bounding volume. For an objective comparison of methods with different conservativity the global time measurement is needed because the results of the VFC in this case affects the load of the output device that can be hardware accelerator or software renderer.
Considering that we did not have all details of the implementation of the same basic VFC algorithm for comparison as the authors of the article, we have used another much less expensive in the term of time that has the same conservativity as the so called Assarson-Möller's basic test (basic intersection) that will be described later. The acceleration can be correctly measured even on less complex scenes by comparison of the CPU needed to compute only the VFC test routines. But we have compared the algorithms with same which producing the same results. The fact that the Möller et al. do not take care about conservativity of the compared algorithms affects reliability of the presented results.
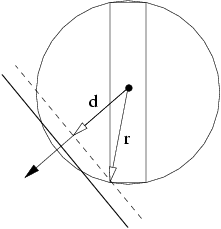
The idea of the basic VFC algorithm for comparison is taken from the article Improved frustum-object cull [6] where Villi Miettinen gives many experiences with the practical applications for solving the VFC problem. His algorithm is optimized for AABB and uses one of the Assarson-Möller's optimization. We used only the core of Miettinen's test without this additional optimization.
The Miettinen's basic VFC algorithm uses the collision detection between the VF and a sphere. In this case the bounding sphere is determined by the center of the AABB and a half of the diagonal connecting the minimal and the maximal vertex of the AABB. So it is sufficient to compute only the distance of the center of the AABB from the tested plane and consists of one dot product and the comparison to the radius of the bounding sphere.
Figure 2 demonstrates the fact that the conversion of the AABB to the bounding sphere is not exact. If we measure the entire radius of the sphere and the distance from the center of the AABB we can see that we only need to compare its projection to the direction of the normal vector of the tested plane. There is one more dot product compared with the simple sphere-plane test. The following pseudo-code describes more implementation details of this method:
int AABBvsFrustum(AABB *b, FRUSTUM *f)
{
float m, n; int i, result = INSIDE;
for (i = 0; i < 6; i++) { PLANE *p = f->plane + i;
m = (b->mx * p->a) + (b->my * p->b) + (b->mz * p->c) + p->d;
n = (b->dx * fabs(p->a)) + (b->dy * fabs(p->b)) + (b->dz * fabs(p->c));
if (m + n < 0) return OUTSIDE;
if (m - n < 0) result = INTERSECT;
} return result;
}
Vector (mx,my,mz) represents the center of the AABB. Absolute values of the normal vector of the plane (a,b,c) transform all possible values to the first octant so its dot product with the vector representing a half of the AABB diagonal (dx,dy,dz) will be always positive.
Three different values are possible as the output of the test that determines the continuation of the rendering pipeline.
OUTSIDE: Bounding box is totally outside of the VF so
the bounded volume is also outside. The object or the dot hierarchy is
eliminated from the further processing.
INSIDE: Bounding box is totally inside of the VF.
There is no need for further culling of the geometry of the bounded
object or down traversal the hierarchy. This state is also useful
information for the software renderer that could avoid the low-level
polygon clipping.
INTERSECT: Object could intersect the VF. The down
traversal the hierarchy is needed and in the case of leafs the sending
of the entire object for culling on the level of the object geometry.
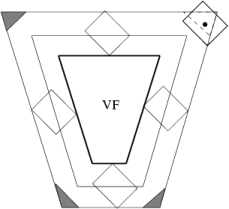
Accuracy of reporting INTERSECT value depends on the
conservativity of the used method. Beside the inaccuracy caused by the
size of the AABB and the size of the bounded object there are another
inaccuracies in the corners of the VF. The algorithm detects the
INTERSECT state even when the bounding volume is in fact
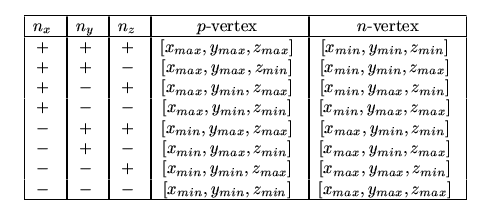
outside the VF. This case is displayed on Figure 3 where the
regions of failure of the algorithm are in edges of sweep frustum.
OUTSIDE, INSIDE, INTERSECT)
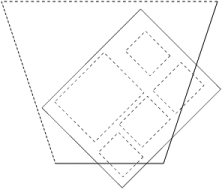
only by the test of two vertices: the n-vertex and the p-vertex.
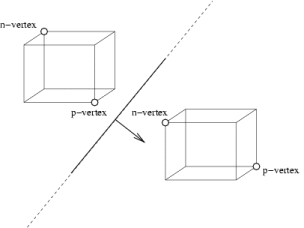
Figure 4 explained the geometric meaning of n,p-vertices. They are defined in the following way: the farthest vertex of the AABB in the positive resp. negative sense in the direction of the normal vector of the plane is the p-vertex resp. n-vertex. Because of the geometry of the AABB it is possible to reduce the determining of the n and p-vertices using look-up Table 1. This table is indexed by the signs of the normal vector parts of the given VF plane.
The basic test uses only two dot products. The first one detects if the n-vertex is outside the half-space defined by actual VF plane. In this case the AABB is also outside VF. If the test fails the next test of the p-vertex is processed. If it is outside then the AABB intersects the plane. In the opposite case the AABB is inside the half-space. The whole algorithm of this basic test is described in the next pseudo-code listing.
Index-vectors (nx,ny,nz) and (px,py,pz) gain min and max vertices. The
implementation of the Table 1 is reduced to 6 values that are
used for indexing of the table of two items with the minimal and
maximal parts of the AABB coordinates. The test for the
OUTSIDE state can be done only by one dot product.
int AABBvsFrustum(AABB *b, FRUSTUM *f)
{
float m, n; int i, result = INSIDE;
for (i = 0; i < 6; i++) { PLANE *p = f->plane + i;
m = (p->a * b->v[p->nx].x) + (p->b * b->v[p->ny].y) + (p->c * b->v[p->nz].z);
if (m > -p->d) return OUTSIDE;
n = (p->a * b->v[p->px].x) + (p->b * b->v[p->py].y) + (p->c * b->v[p->pz].z);
if (n > -p->d) result = INTERSECT;
} return result;
}
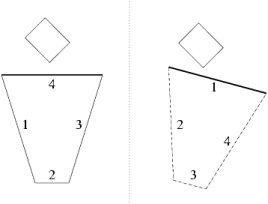
To take advantages of the hierarchy the authors invented an incremental reduction of planes that are needed to test for collision with the AABB in the given level of hierarchy. If the parent bounding box is inside the half-space then this test is not needed in lower levels of the hierarchy. Each child is then also inside this half-space. See Figure 5.
In the recursive traversal the bit-mask of the planes is sent from a
parent to its children. In the position of the second dot product that
is used for determining the INTERSECT state the plane is
masked out in the case of the negative test for the elimination of
further tests on the next levels of the hierarchy.
int AABBvsFrustum(AABB *b, FRUSTUM *f, int in_mask, int *out_mask)
{
float m, n; int i, k, result = INSIDE; *out_mask=0;
for (i = 0, k = 1; k <= in_mask; i++, k += k) if (k & in_mask) {
PLANE *p = f->plane + i;
m = (p->a * b->v[p->nx].x) + (p->b * b->v[p->ny].y) + (p->c * b->v[p->nz].z);
if (m > -p->d) return OUTSIDE;
n = (p->a * b->v[p->px].x) + (p->b * b->v[p->py].y) + (p->c * b->v[p->pz].z);
if (n > -p->d) { *out_mask |= k; result = INTERSECT; }
} return result;
}
int AABBvsFrustum(AABB *b, FRUSTUM *f, int in_mask, int *out_mask)
{
float m, n; int i, k = 1 << b->start_id, result = INSIDE;
PLANE *sp = f->plane + b->start_id; *out_mask=0;
if (k & in_mask) {
m = (sp->a * b->v[sp->nx].x) + (sp->b * b->v[sp->ny].y) + (sp->c * b->v[sp->nz].z);
if (m > -sp->d) return OUTSIDE;
n = (sp->a * b->v[sp->px].x) + (sp->b * b->v[sp->py].y) + (sp->c * b->v[sp->pz].z);
if (n > -sp->d) { *out_mask |= k; result = INTERSECT; }
}
for (i = 0, k = 1; k <= in_mask; i++, k += k)
if ((i != b->start_id) && (k & in_mask)) { PLANE *p = f->plane + i;
m = (p->a * b->v[p->nx].x) + (p->b * b->v[p->ny].y) + (p->c * b->v[p->nz].z);
if (m > -p->d) { b->start_id = i; return OUTSIDE; }
n = (p->a * b->v[p->px].x) + (p->b * b->v[p->py].y) + (p->c * b->v[p->pz].z);
if (n > -p->d) { *out_mask |= k; result = INTERSECT; }
} return result;
}
Möller et al. do not give more detailed description of the implementation so we could not implement the octant test to be as good as the authors present. The problem is that the octant that the AABB center belongs to could be determined only by three dot products. This means permanent loss of nine multiplications before the test with the first plane. The next problem is the test of the functionality of the octant test. The comparison of two distances are needed that are computed after any change in the geometry of the AABB and the VF. These computations are called heavily in dynamic scenes so after the activating of this test the VFC is slowed down. Because of this we do not find this test useful and we will not introduce its relatively complicated implementation.
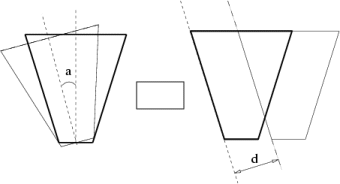
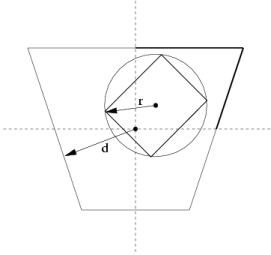
a where a is the angle between
the left and right plane of the VF.
d. We compute the projection of this
increment to the directions of the normal vectors of all VF planes.
Before the test for a collision of the given bounding volume with the
VF plane we compare the distance to the given plane from the last
frame with the current increment. If the increment is greater than
this distance the collision detection with the given plane has to be
processed.
As an input the internal format of the 3D Studio 4.0 was chosen. It has all necessary properties mainly for scene motion. The application supports animation based on the interpolation of the quaternions using Kochanek-Bartels piece-wise continuous spline functions. The hierarchy of the AABBs is automatically actualized. The AABB hierarchy is generated from the current OBB leafs by a transformation.

The user can watch the scene from the point above the scene or directly by the view of the tested camera. All eight degrees of freedom and the geometry can be controlled by a mouse or by hot keys. The current state of the VFC algorithm can be seen in the output window (see Figure 9). Each of the six camera planes has its own color that is used for coloring the objects that collide with this plane. Objects inside the VF are of white color and objects outside are not displayed at all. The current used level of the hierarchy can be seen on the displayed AABBs. The algorithm can be switched to the collision detection mode where the VFC test is applied to the bounding box chosen by a user.
The OpenGL application was compiled using GCC 3.0 under Linux and Windows (MinGW 1.1). For measurement reasons more functions with different optimization are run simultaneously and the time is measured for each of them. The obtained results is then sent using TCP/IP to the independent application (it can be on another computer) that takes care about their processing and displaying.
vfc.3ds) is smaller in the number of triangles and the camera
flies over the entire scene. The second scene (big.3ds)
is more complex. The camera flies over the entire scene and in one
case even outside it.The measurement was processed in two modes. The first mode (see Graph 1 and Graph 3) represents the influence of a motion of the camera and the objects movement on the VFC efficiency. In the second mode (see Graph 2 and Graph 4) the animation of the objects is disabled in the whole scene. All measurements were performed in the 200-frames animation where in each of the frame different optimization of the VFC algorithm were applied. The measured time is shown relative to the time of the basic VFC algorithm without any hierarchy. The results are in the graphs where is shown time dependency and in the tables where there are the average values for the entire measurement.
vfc.3ds scene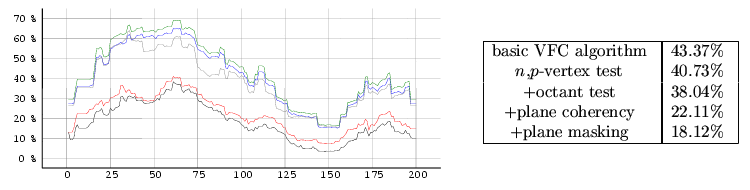
vfc.3ds - full objects motion.
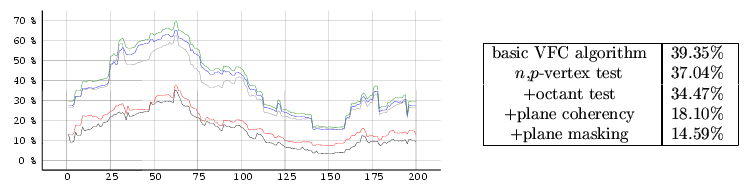
vfc.3ds - without animation.
big.3ds scene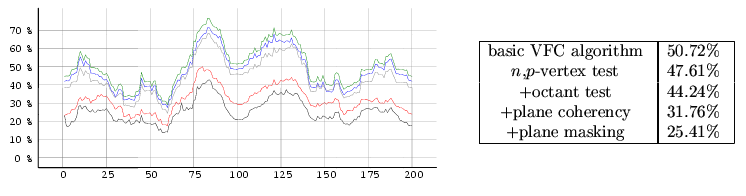
big1.3ds - full objects motion.
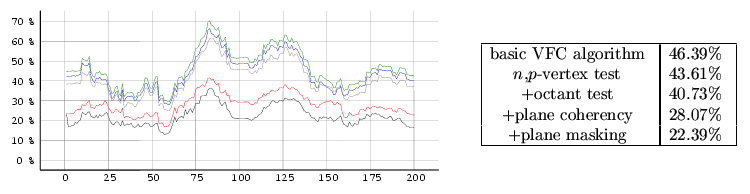
big2.3ds - without animation.| [1] | Ulf Assarson and Tomas Möller. Optimized View Frustum Culling Algorithms for Bounding Boxes. In Journal of Graphics Tools, 5(1), pages 9-22, 2000. |
| [2] | James H. Clark. Hierarchical Geometric Models for Visible Surface Algorithms. In Communications of the ACM 19(10), pages 547-554, 1976. |
| [3] | Mel Slater and Yiorgos Chrysanthou. View Volume Culling Using a Probabilistic Caching Scheme. In Proceedings of the ACM Symposium on Virtual Reality Software and Technology, pages 71-78, 1997. |
| [4] | Jiøí Bittner and Vlastimil Havran, Exploiting Temporal and Spatial Coherence in Hierarchical Visibility Algorithms. In Proceedings of Spring Conference on Computer Graphics, Budmerice, SK, 2001. |
| [5] | Ulf Assarson and Tomas Möller. Optimized View Frustum Culling Algorithms (technical report 99-3). Chalmers University of Technology, Sweden 1999. |
| [6] | Villi Miettinen. Improved frustum-object cull. In Sourceforge mailing list, gdAlgorithms-list, 2000. |
| [7] | J.T. Klosowski, M. Held, J.S.B. Mitchell, H. Sowizral and K. Zikan. Efficient Collision Detection Using Bounding Volume Hierarchies of k-DOP. In IEEE Transactions on Visualization and Computer Graphics, 4(1), pages 21-36, 1998. |