Monte-Carlo Global Illumination Rendering
László Szirmay-Kalos
szirmay@iit.bme.hu
Department of Control Engineering and Information Technology
Budapest University of Technology
Budapest / Hungary
This talk examines the global illumination problem and classifies its
solution alternatives as random walks and iteration. Random walk algorithms
reflect the real phenomena while iteration can efficiently utilize
the hardware and smooth the solution, thus they offer very different
flexibility and speed.
The primary candidates of the efficient solutions
are presented, emphasizing the open problems and the future
improvement possibilities.
KEYWORDS: global illumination, random walk, iteration.
Global illumination rendering is preferred in many graphics applications where
realism is a primary issue. However, its application is limited due to
the enormous computational requirements and long rendering times.
The fundamental difficulty of the global illumination problem is
that the illumination of a point
may stem from infinitely many other points.
Since it is impossible to work with infinite data,
we always have to select a finite part, which requires sampling.
Thus sampling the illumination attached
to complex geometric structures is the basic operation of
global illumination algorithms.
The question is how the samples should be generated in order to make the computation fast.
There are two orthogonal approaches to answer this question.
According to the first approach, the samples should be obtained in a way which is optimal
from the point of view of the problem to be solved.
Random walk algorithms usually follow this direction.
Since the global illumination problem is high-dimensional
(a ligh-path connecting the light sources to the eye via reflections and
refractions can be described by a lot of, i.e. 10-20, scalars),
the classical sampling based on regular grids becomes very inefficient.
These regular grids are very uneven in higher dimensions,
resulting in a requirement that the number of samples must be an
exponential function of the dimension of the domain.
Generating the samples randomly or quasi-randomly following,
for example, a Halton series, this dimensional explosion can be avoided.
This is a basic idea of Monte-Carlo methods.
The error of the Monte-Carlo methods can be minimized if the sampling is proportional
to the illumination carried by the sample (importance sampling).
The problem is that in many cases we do not know this illumination without generating the sample,
thus importance sampling can only be approximately met.
The fundamental advantage of the random walk approach is that it suits to the problem to be solved,
thus the algorithm is general, all properties (ideal reflectors, refractors, textures, etc.)
can easily be taken into account, and the implementation is also relatively simple.
Even the complexity is quite good, the computation time is usually logarithmic with
a small constant scaling of the logarithm function
(or even constant if the scene contains objects that are reasonably uniformly distributed),
after a preprocessing step that is usually quadratic
or at least in
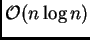 .
In this talk we study gathering and shooting algorithms and their combination.
Gathering starts
at the eye and tries to locate the light sources, from where the emission can be transferred to
the eye. We concluded that the error of gathering algorithms can be very large if the light sources
are small. Shooting algorithms, on the other hand, start at the light sources and generate
light path similarly as happens in real world. Shooting can have very large error if
we have a small aperture camera.
In order to attack this problem, gathering algorithms apply shadow rays from each
visited point towards to light sources, and shooting methods connect
the visited points with the camera deterministically.
These correspond to replacing the light sources and the measuring function by
their first reflections, respectively, which are usually much bigger and more uniform.
In this way, the
sizes of the light sources and the eye are increased virtually.
Bi-directional path tracing generalizes this idea even further, and randomly
expands both the light sources and the pin hole camera.
Thus bi-directional path tracing can be much better than either gathering and shooting.
The other common problem of these techniques is that they cannot exploit coherence or the similarity of the
regions in the space of light path. When a light path is established and its contribution is
determined, the light path is thrown away and a new path is generated from scratch.
According to the practical experiments, we can say that the number of samples
can be as high as several hundred or about one thousand, even for relatively simple scenes and
lighting conditions.
Metropolis sampling offers an elegant way to reuse previous information, namely the last path.
According to the error
analysis, Metropolis can render good images with 100-200 samples per pixel even if the lighting
situation is difficult.
Photon map methods, on the other hand, allow the exploitation of the coherence and the reuse
of the previous information on a much higher level.
The computational burden of the Photon map algorithm is
equivalent to computing less than a hundred light paths per pixel.
On the other hand, we have to pay a price for exploiting coherence and reusing previous
information. Namely, Photon map is only an approximate technique, unlike classical random walks
and the Metropolis algorithm, which guarantee asymptotic accuracy.
Photon map belongs to the category of those algorithms that trade
the asymptotic accuracy, also called unbiasedness, for speed. The promising idea
of trading bias for noise could
be applied in many other algorithms and has not been fully explored yet.
We believe
that real-time global illumination will only be possible for these approximate techniques
in the next few years.
The approximate character is not a problem until it does not generate visible artifacts on the
image. Considering the fact, that the direct illumination has the highest variation and is
responsible for sharper shadows, etc. these artifacts should be eliminated primarily at the
direct illumination and high importance points. The effects of indirect illumination and higher
order reflections are much smoother, thus we can use approximations here more intensively.
The advanced final gathering algorithms of Photon map meet this requirement, when they decide at
each point whether the radiance is computed from the photon hits (approximation) or the
radiance is obtained
by Monte-Carlo integration (asymptotically correct approach).
In the second approach the samples are obtained in a way which is optimal
for the current (graphics) hardware. This idea is used usually in iteration algorithms.
Classical finite-element based iteration algorithms have enormous memory
requirements since the directional dependent radiance function should be stored on
each patch. Randomization can attack this problem, which resulted
in a stochastic iteration scheme.
In stochastic iteration those samples are collected, which correspond, for example,
to parallel rays or to rays joining at the same point, and
parallel or perspective bundles are formed.
The main advantage of this approach is that it can exploit the coherence of the scene
(neighboring points are usually similar), and even if no graphics acceleration is available,
these methods generate coherent memory access which is good for the general purpose processors as well.
Parallel ray-bundle stochastic iteration transfers
the radiance of all points in the scene parallel to a randomly selected global
direction. This random selection allows us to store just
a single or a few radiance values instead of storing the complete directional
radiance function on each patch. As all iteration techniques, stochastic
iteration uses finite-element decomposition, which breaks down the surfaces
to planar patches and assumes that these patches have uniform radiance.
Parallel ray-bundles are efficient if there are large light sources. This requirement
can be met if the first reflection of the light is computed with deterministic techniques, which
leads to the idea of first shot.
Currently, for moderately complex scenes (10-50 thousand patches) the first shot takes a few seconds,
then the algorithm renders the scene in a few tens of seconds. Larger scenes consisting of
a few hundred thousand patches can be rendered in 5-10 minutes. However, we have to admit
that these methods require the polygons to be tessellated to patches, which increases the
scene complexity and can result in exausting the physical memory.
Perspective ray-bundle iteration, on the other hand, transfers the radiance of a
randomly selected patch in all possible directions using the classical hemicube.
The hemicube transfer can easily be supported by the hardware z-buffer.
In order to eliminate the random noise, we proposed a new technique that trades bias for noise.
The idea is that when a very unlikely event happens during the random simulation
(the calculated probability is very small compared to the number of samples),
then this sample is ignored. Unlike parallel ray-bundle iteration, this method does not require first shot.
Its performance seems to be similar to that of the parallel ray-bundle technique.
Stochastic iteration algorithms do not need preprocessing,
but the complexity of the rendering is at least linear.
Using current hardware, such approaches allow the global illumination rendering of
moderately complex scenes (10-100 thousand patches) in less than a minute.
However, special features, such as ideal reflections and refractions
may pose problems to these methods that are good only
for diffuse and glossy (i.e. moderately specular) scenes.
The parallelization is not as trivial as in random walk algorithms but is possible and
the expected speed-up is linear until about 8-16 processors.
In order to exploit coherence, these algorithms apply assumptions that some smaller parts (called patches)
of the scene behave similarly. Of course, this can be responsible for high speed-ups, but can result
in artifacts as well. As we have seen in photon maps, such artifacts can be eliminated without sacrificing
the speed if the direct reflection is computed with more accurate techniques.
The direct reflection can be determined
with classical Phong-shading and we can apply the
results of stochastic iteration just for indirect
illumination. In order to achieve real-time behavior, the very old Phong shading and shadow
computation should also be revisited and speeded up.
Thus the research of global illumination algorithms should also consider these
non-global illumination problems as well.
Random walk and iteration algorithms have different priorities, thus they have
different complexity, flexibility and speed. Due to the fact that iteration can
exploit coherence and the graphics hardware, it is currently much faster, but
have severe limitations. However,
if coherence could be more efficiently used in random walks and future computer
architectures would be more appropriate for incoherent sampling, then random walks
could be real alternatives even in interactive applications.
.
In this talk we study gathering and shooting algorithms and their combination.
Gathering starts
at the eye and tries to locate the light sources, from where the emission can be transferred to
the eye. We concluded that the error of gathering algorithms can be very large if the light sources
are small. Shooting algorithms, on the other hand, start at the light sources and generate
light path similarly as happens in real world. Shooting can have very large error if
we have a small aperture camera.
In order to attack this problem, gathering algorithms apply shadow rays from each
visited point towards to light sources, and shooting methods connect
the visited points with the camera deterministically.
These correspond to replacing the light sources and the measuring function by
their first reflections, respectively, which are usually much bigger and more uniform.
In this way, the
sizes of the light sources and the eye are increased virtually.
Bi-directional path tracing generalizes this idea even further, and randomly
expands both the light sources and the pin hole camera.
Thus bi-directional path tracing can be much better than either gathering and shooting.
The other common problem of these techniques is that they cannot exploit coherence or the similarity of the
regions in the space of light path. When a light path is established and its contribution is
determined, the light path is thrown away and a new path is generated from scratch.
According to the practical experiments, we can say that the number of samples
can be as high as several hundred or about one thousand, even for relatively simple scenes and
lighting conditions.
Metropolis sampling offers an elegant way to reuse previous information, namely the last path.
According to the error
analysis, Metropolis can render good images with 100-200 samples per pixel even if the lighting
situation is difficult.
Photon map methods, on the other hand, allow the exploitation of the coherence and the reuse
of the previous information on a much higher level.
The computational burden of the Photon map algorithm is
equivalent to computing less than a hundred light paths per pixel.
On the other hand, we have to pay a price for exploiting coherence and reusing previous
information. Namely, Photon map is only an approximate technique, unlike classical random walks
and the Metropolis algorithm, which guarantee asymptotic accuracy.
Photon map belongs to the category of those algorithms that trade
the asymptotic accuracy, also called unbiasedness, for speed. The promising idea
of trading bias for noise could
be applied in many other algorithms and has not been fully explored yet.
We believe
that real-time global illumination will only be possible for these approximate techniques
in the next few years.
The approximate character is not a problem until it does not generate visible artifacts on the
image. Considering the fact, that the direct illumination has the highest variation and is
responsible for sharper shadows, etc. these artifacts should be eliminated primarily at the
direct illumination and high importance points. The effects of indirect illumination and higher
order reflections are much smoother, thus we can use approximations here more intensively.
The advanced final gathering algorithms of Photon map meet this requirement, when they decide at
each point whether the radiance is computed from the photon hits (approximation) or the
radiance is obtained
by Monte-Carlo integration (asymptotically correct approach).
In the second approach the samples are obtained in a way which is optimal
for the current (graphics) hardware. This idea is used usually in iteration algorithms.
Classical finite-element based iteration algorithms have enormous memory
requirements since the directional dependent radiance function should be stored on
each patch. Randomization can attack this problem, which resulted
in a stochastic iteration scheme.
In stochastic iteration those samples are collected, which correspond, for example,
to parallel rays or to rays joining at the same point, and
parallel or perspective bundles are formed.
The main advantage of this approach is that it can exploit the coherence of the scene
(neighboring points are usually similar), and even if no graphics acceleration is available,
these methods generate coherent memory access which is good for the general purpose processors as well.
Parallel ray-bundle stochastic iteration transfers
the radiance of all points in the scene parallel to a randomly selected global
direction. This random selection allows us to store just
a single or a few radiance values instead of storing the complete directional
radiance function on each patch. As all iteration techniques, stochastic
iteration uses finite-element decomposition, which breaks down the surfaces
to planar patches and assumes that these patches have uniform radiance.
Parallel ray-bundles are efficient if there are large light sources. This requirement
can be met if the first reflection of the light is computed with deterministic techniques, which
leads to the idea of first shot.
Currently, for moderately complex scenes (10-50 thousand patches) the first shot takes a few seconds,
then the algorithm renders the scene in a few tens of seconds. Larger scenes consisting of
a few hundred thousand patches can be rendered in 5-10 minutes. However, we have to admit
that these methods require the polygons to be tessellated to patches, which increases the
scene complexity and can result in exausting the physical memory.
Perspective ray-bundle iteration, on the other hand, transfers the radiance of a
randomly selected patch in all possible directions using the classical hemicube.
The hemicube transfer can easily be supported by the hardware z-buffer.
In order to eliminate the random noise, we proposed a new technique that trades bias for noise.
The idea is that when a very unlikely event happens during the random simulation
(the calculated probability is very small compared to the number of samples),
then this sample is ignored. Unlike parallel ray-bundle iteration, this method does not require first shot.
Its performance seems to be similar to that of the parallel ray-bundle technique.
Stochastic iteration algorithms do not need preprocessing,
but the complexity of the rendering is at least linear.
Using current hardware, such approaches allow the global illumination rendering of
moderately complex scenes (10-100 thousand patches) in less than a minute.
However, special features, such as ideal reflections and refractions
may pose problems to these methods that are good only
for diffuse and glossy (i.e. moderately specular) scenes.
The parallelization is not as trivial as in random walk algorithms but is possible and
the expected speed-up is linear until about 8-16 processors.
In order to exploit coherence, these algorithms apply assumptions that some smaller parts (called patches)
of the scene behave similarly. Of course, this can be responsible for high speed-ups, but can result
in artifacts as well. As we have seen in photon maps, such artifacts can be eliminated without sacrificing
the speed if the direct reflection is computed with more accurate techniques.
The direct reflection can be determined
with classical Phong-shading and we can apply the
results of stochastic iteration just for indirect
illumination. In order to achieve real-time behavior, the very old Phong shading and shadow
computation should also be revisited and speeded up.
Thus the research of global illumination algorithms should also consider these
non-global illumination problems as well.
Random walk and iteration algorithms have different priorities, thus they have
different complexity, flexibility and speed. Due to the fact that iteration can
exploit coherence and the graphics hardware, it is currently much faster, but
have severe limitations. However,
if coherence could be more efficiently used in random walks and future computer
architectures would be more appropriate for incoherent sampling, then random walks
could be real alternatives even in interactive applications.
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.43)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -no_navigation invited_talk_ceszkl.tex