Robust Automatic Registration of Range Images with Reflectance
Marcel Körtgen
Computer Graphics Group, Institute of Computer Science II, University of Bonn/Germany
Email: koertgen@cs.uni-bonn.de
Web: http://cg.cs.uni-bonn.de
Abstract
We tackle the problem of automatic matching, consistency checking and registration of multiple unknown and unordered range images. Utilizing robust visual features extracted from the supplied reflectance images, an efficient pairwise view matching scheme is used to build up a directed correspondence graph, nodes representing the input range images and edges labeled with relative pose estimates. Subsequently, a local and global consistency check eliminate false positive edges in the graph as these prevent the succeeding to a correct solution. Absolute poses are recovered by a breadth-first search (BFS), thereby, for each visited node, combining the weighted contributions of all encountered paths back to the root. Remarkably, the absolute alignments are accurately recovered from only the features. Thus, a subsequent fine registration step can be omitted. The framework is independent from object size and particular sensor model.Introduction
Registration has been an active topic of research for about thirty years. Much work in the past successfully addressed pairwise registration, i.e. aligning two three-dimensional (3d) views of a static scene. Due to the ongoing advances in scanning and computer hardware for about the last ten years, multiple view registration became manageably and thus more and more attractive as a basic tool in reconstructing a complete 3d model from a captured scene. However, most multiview approaches assume that the input views are roughly prealigned or that it is known which views overlap one another. In contrast, just a small amount of research has been published that engages automatic matching, consistency checking and registration of multiple unknown views as presented here. Today, a laser range scanner is the method of choice for digitizing real-world objects of moderate size. Laser range scanners are non-contact 3d scanners that measure the distance from the sensor to points in the scene, typically in a regular grid pattern. A range image is the visualization of this grid pattern where the pixel intensity is a function of the measured distance (cf. figure 1). A natural byproduct of the acquisition process is the reflectance image that records the laser reflectance strength (LRS) for each pixel.

Figure 1: a) A range image (left) obtained with the Z+F Imager 5003 and corresponding co-registered reflectance image (right). b) A range image (left) obtained with the Minolta Vivid 900 and gray-scaled color image (right).
In general, because of occlusion and field of view limitations, not all parts of the scene can be observed from any given position. Therefore, range data from multiple viewpoints must be combined to form a complete model of the scene. Given a set of n overlapping range images of a static scene, the process of creating the complete scene model consists of two main steps: registration and reconstruction. In the registration step, the n input range images are all aligned in a common coordinate system whereas the reconstruction step usually accounts for the generation of a triangulated mesh out of the registered range data. We concentrate on the registration step because this is where the central automation issues lie.Paper
Download the full paper: paper.pdf.
Download the bibtex-file: paper.bib.
Images and Results
Some images and results not shown in the paper (See [16] instead).| Spherical Scans (Z+F Imager 5003) | |
|---|---|
 Resampling to 8 overlapping perspective range images. |
 6 spherical scans registered (48 range images; 512x512 resolution each). |
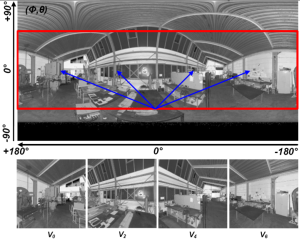
However, by the time of writing the implementation of the SIFT detector [25] (http://www.cs.ubc.ca/~lowe/keypoints/) was neither suitable for non-perspective images nor resolutions of more than about 1.800 pixels in any dimension. We therefore partition the spherical images into n=2x4 perspective range images (512x512 each), by sequential rotations of 45° about the up-vector and subsequent projection on an image plane with a 90° field of view, both horizontally and vertically. In order to avoid missing features or cutting them in two, each perspective view overlaps half of the adjacent views. In this manner, each spherical view is decomposed into a graph component of 8 perspective range images that are already registered with respect to the considered spherical view.
| Observation confidence for range measurements | |
|---|---|
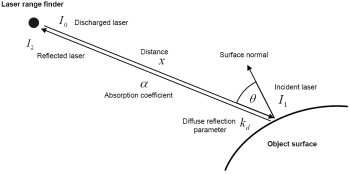 Dichromatic reflection model as proposed by [32]. |
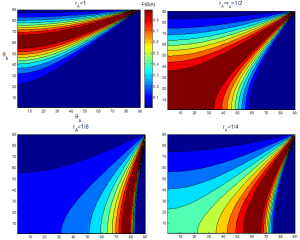 Contour plots of conditional pixel confidences. |
For a surface (a pixel) observed in range image A, the likelihood of observation is modeled as a gaussian of the measured reflectance. The location parameter (or the mean) of the gaussian represents the calibrated reflectance of the device.
The scale parameter (or the standard deviation) represents the range of reflectances around the mean that can be confidently handled by the device. For reflectances higher than the mean one needs to consider blooming whereas the case for reflectances lower than the mean is suspect to undersaturation.
When surface/point normals are available the dichromatic reflectance model can be used to infer the "warped" reflectance, i.e. the reflectance of the same pixel as seen from the viewpoint of range image B. Feeding this warped reflectance value into the gaussian yields the conditional observation confidence P(A|B), which is shown above for varying normal-eye-angles and measured reflectances in image A. Note that reflectances are scaled to [0,1].
The question remains how to select proper values for location and scale of the gaussian. If the device is well known or directly available, these values can be derived from the technical specifications or obtained by a calibration experiment. Otherwise, we propose maximum-likelihood estimation from an accumulative reflectance histogram of the input set.
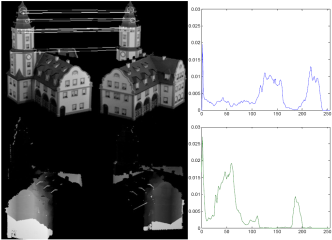
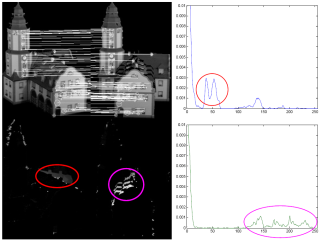
- Typically, for inconsistent matches, no single peak dominates the distribution. Here, the mode at bin 0 takes only 3.75% (blue) and 1.66% (green) of the total number of observations. Note that the vertical axis has been clamped at 3%. In general, the numbers, locations and heights of the distribution peaks are unpredictable due to the varying complexity of the captured geometry. It is definitely challenging and might probably be impossible to find a general model that is able to describe the distribution of distances for inconsistent matches.
- The distribution of the surface distances for consistent matches is typically well behaved. This is because small surface distances corresponding to consistent surfaces dominate the whole distribution. Here, bin 0 takes 45% (blue) and 52% (green) of the total number of observations. Note that the vertical axis has been clamped at 1% so that less frequent distances are better visible (typically 0.1%). Indeed, the small bumps (red and pink surrounded regions) result from the shadowing effect (see e.g. [5]) which has not been modeled in this preliminary experiment.
Video
Download the real-time rendering video of the registered 3d pointcloud shown in the paper:
church-divx521.avi.
(c) Marcel Körtgen
References
Download the bibtex-file: paper.bib
-
[1]
- Nina Amenta, Sunghee Choi, and Ravi Krishna Kolluri. The power crust, unions of balls, and the medial axis transform. Computational Geometry, 19(2-3):127-153, 2001. [2]
- T. Dey and S. Goswami. Tight cocone: A water-tight surface reconstructor, 2003. [3]
- P. J. Besl and N. D. McKay. A method for registration of 3-D shapes. IEEE Transactions on Pattern Analysis and machine Intelligence, 14(2):239-258, February 1992. [4]
- Szymon Rusinkiewicz and Marc Levoy. Efficient variants of the ICP algorithm. In Proceedings of the Third Intl. Conf. on 3D Digital Imaging and Modeling, pages 145-152, 2001. [5]
- Daniel Huber. Automatic Three-dimensional Modeling from Reality. PhD thesis, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, December 2002. [6]
- Peter Biber and Wolfgang Straßer. Solving the correspondence problem by finding unique features. In 16th International Conference on Vision Interface, 2003. [7]
- S. Gumhold, X. Wang, and R. McLeod. Feature extraction from point clouds, 2001. [8]
- M. Pauly, R. Keiser, and M. Gross. Multi-scale feature extraction on point-sampled surfaces, 2003. [9]
- Gregory C. Sharp. Automatic and Stable Multiview 3D Surface Registration. PhD thesis, University of Michigan, Oct 2002. [10]
- Gerhard H. Bendels, Patrick Degener, Roland Wahl, Marcel Körtgen, and Reinhard Klein. Image-based registration of 3d-range data using feature surface elements. In VAST, pages 115-124, 2004. [11]
- Xinju Li and Igor Guskov. Multiscale features for approximate alignment of point-based surfaces. In Symposium on Geometry Processing, pages 217-226, 2005. [12]
- N. Gelfand, N. J. Mitra, L. J. Guibas, and H. Pottmann. Robust global registration. In Symposium on Geometry Processing, pages 197-206, 2005. [13]
- Shankar Krishnan, Pei Yean Lee, John B. Moore, and Suresh Venkatasubramanian. Global registration of multiple 3d point sets via optimization-on-a-manifold. In Symposium on Geometry Processing, pages 187-196, 2005. [14]
- Ameesh Makadia, Alexander Patterson, and Kostas Daniilidis. Fully automatic registration of 3d point clouds. In IEEE Conference on Computer Vision and Pattern Recognition,, 2006. [15]
- Peter Biber and Wolfgang Strasser. nscan-matching: Simultaneous matching of multiple scans and application to slam. In IEEE International Conference on Robotics and Automation, 2006. [16]
- Marcel Körtgen. Robust automatic registration of range images with reflectance. Diploma thesis, Computer Graphics Institute, University of Bonn, Germany, 2006. Available at http://marcel.koertgen.de/marcy/research/2006/da-koertgen-2006.pdf. [17]
- Bradford J. King, Tomasz Malisiewicz, Charles V. Stewart, and Richard J. Radke. Registration of multiple range scans as a location recognition problem: Hypothesis generation, refinement and verification. In 3DIM, pages 180-187, 2005. [18]
- Devrim Akca. Full automatic registration of laser scanner point clouds. In A. Gruen and H. Kahmen, editors, Optical 3-D Measurement Techniques VI, volume 1, pages 330-337, 2003. [19]
- Gerard Blais and Levine Martin. Registering multiview range data to create 3D computer objects. Technical Report CIM-93-16, McGill Centre for Intelligent Machines, March 1994. [20]
- Xavier Pennec. Multiple Registration and Mean Rigid Shapes - Application to the 3D case. In I.L. Dryden K.V. Mardia, C.A. Gill, editor, Image Fusion and Shape Variability Techniques (16th Leeds Annual Statistical (LASR) Workshop), pages 178-185, july 1996. [21]
- David W. Eggert, Andrew W. Fitzgibbon, and Robert B. Fisher. Simultaneous registration of multiple range views for use in reverse engineering of cad models. Comput. Vis. Image Underst., 69(3):253-272, 1998. [22]
- Chitra Dorai, Gang Wang, Anil K. Jain, and Carolyn Mercer. Registration and integration of multiple object views for 3d model construction. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20(1):83-89, 1998. [23]
- S.J. Cunnington and A.J. Stoddart. N-view point set registration: A comparison. In British Machine Vision Conference, volume 1, pages 234-244, Nottingham, UK, 1999. [24]
- Kari Pulli. Multiview registration for large data sets. In Proceedings of the International Conference on 3D Digital Imaging and Modeling, pages 160-168, 1999. [25]
- David Lowe. Distinctive image features from scale-invariant keypoints, 2003. [26]
- Krystian Mikolajczyk and Cordelia Schmid. A performance evaluation of local descriptors. IEEE Transactions on Pattern Analysis & Machine Intelligence, 27(10):1615-1630, 2005. [27]
- J. Beis and D. Lowe. Shape indexing using approximate nearest-neighbor search in highdimensional spaces, 1997. [28]
- Berthold K. P. Horn. Closed-form solution of absolute orientation using unit quaternions. Journal of the Optical Society of America A, 4(4):629-642, April 1987. [29]
- Leonard McMillan. An Image-Based Approach to Three-Dimensional Computer Graphics. PhD thesis, University of North Carolina, Apr 1997. [30]
- Reinhard Diestel. Graph Theory, volume 173. Springer-Verlag, Heidelberg, 3 edition, July 2005. [31]
- Charles Bloom, Jonathan Blow, and Casey Muratori. Errors and omissions in marc alexa´s "linear combinations of transformations", 2004. Available at http://www.cbloom.com/3d/techdocs/lcot_errors.pdf. [32]
- Ryusuke Sagawa, Ko Nishino, and Katsushi Ikeuchi. Adaptively merging largescale range data with reflectance properties. IEEE Trans. Pattern Anal. Mach. Intell., 27(3):392–405, March 2005.