
|
Comenius University |
| Faculty of Mathematics, Physics and Informatics | |
| Department of Applied Informatics |
|
||
| Extraction of skinning data by mesh contraction with Collada 1.5 support | ||
| by Martin Madaras | ||
Abstract
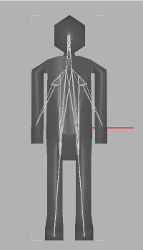
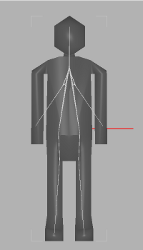
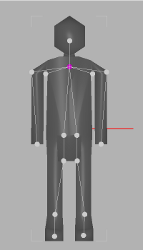
The most common approach to animate models and determine their shape attributes in computer graphics is using skeletons. The skeleton and skinning weights can be either assigned manually or computed from an input mesh. This paper proposes the extraction of a skeleton and skinning weights from a mesh, describes how to store computed data in Collada 1.5 and use it for an animation. Firstly, the mesh is contracted using constrained Laplacian smoothing in a few iterations. Then the most important vertices from the contracted mesh are chosen as control points. Multiple edges are removed and vertices that are very close to each other are merged. We select and collapse a vertex pair with the minimum cost in every iteration using a greedy algorithm. The greedy selection is applied repeatably until we have the requested number of bones. In the next step the skinning weights are computed, according to if we want rigid or soft skinning. In the postprocessing stage the user can test the skeleton by skinning the mesh, make desired changes and export the skeleton to Collada 1.5. Transformation matrices used in a hierarchical skeleton tree are not transformed to joint's local transformation frame, so they are immediately compatible with majority of animation software and libraries. After the Collada file with the mesh, the skeleton and skinning data is exported, data can be imported in animation software such as 3D Studio Max, Blender or Maya and a skinning animation can be rendered.
Results
We have tested the framework on a wide range of different models. We have achieved good results with both high resolution and also with low resolution models. The more vertices the model has, the better skeleton can be computed but the algorithm takes more time. Also the low resolution models (less than 5000 polygons) can be contracted in a good way, but it is harder to set good contraction weights. Setting the right contraction weights is the most problematic part of this approach. Low resolution models are more sensitive for high curvature differences and can be easily over contracted. Weights often have to be set manually and the user needs some experience. Contraction of high resolution models is more deterministic and good weights can be set automatically. After the comparison we can conclude that the extracted skeleton is very close to the manually rigged one. It can be used as a sufficient supplicant for a manually created and rigged skeleton. The major difference can be observed on the both ends of the worm and in the largest bend. Nodes of the skeleton tree were pushed into their centers of local mesh areas and that is why they were pushed inside, away from the mesh boundary.






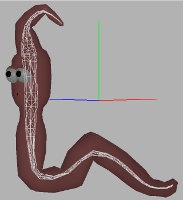

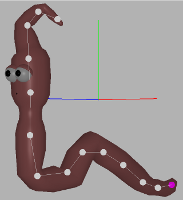
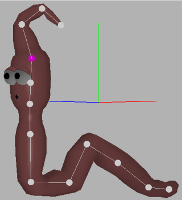




References
[1] O. Kin-Chung Au, Chiew-Lan Tai, Hung-Kuo Chu, D. Cohen-Or, and Tong-Yee Lee. Skeleton extraction by mesh contraction. ACM Transactions on Graphics, 27(3), aug 2008.
[2] G. Aujay, F. Hetroy, F. Lazarus, and Ch. Depraz. Harmonic skeleton for realistic character animation. Symposium on Computer Animation, 2007.
[3] Norman I. Badler, Kamran H. Manoocherhri, and Grahm Walters. Articulated figure positioning by multiple constraints. IEEE Transactions on Visualization and Computer Graphics, 7:28–38, jun 1987.
[4] Paolo Baerlocher and Ronan Boulic. An inverse kinematics architecture enforcing an arbitrary number of strict priority levels. The Visual Computer, 20(6):402–417, jun 2004.
[5] Ronan Boulic, Ramon Mas-Sanso, and Daniel Thalmann. Complex character positioning based on a compatible flow model of multiple supports. IEEE Transactions on Visualization and Computer Graphics, 3:245–261, jul 1997.
[6] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, pages 558–565. MIT Press and McGraw- Hill, first edition, 1990.
[7] Nicu D. Cornea, Deborah Silver, and Patrick Min. Curve-skeleton properties, applications, and algorithms. IEEE Transactions on Visualization and Computer Graphics, 13:530–548, may 2007.
[8] Mathieu Desbrun, Mark Meyer, Peter Schroder, and Alan H. Barr. Implicit fairing of irregular meshes using diffusion and curvature flow. Proceedings of ACM SIGGRAPH 99, 1999.
[9] Tamal K. Dey and Jian Sun. Defining and computing curve-skeletons with medial geodesic function. Eurographics Symposium on Geometry Processing, 256:143–152, 2008.
[10] Michael Garland and Paul S. Heckbert. Surface simplification using quadric error metrics. International Conference on Computer Graphics and Interactive Techniques, pages 209 – 216, 1997.
...
Download full paper
Download poster (90x90cm)