 and dithered voxel intensity of the same voxel is
and dithered voxel intensity of the same voxel is 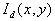 ,
we can defined, that
,
we can defined, that 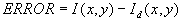 .
. Ing. Petr Chlumsky
e-mail: chlumsky@cslab.felk.cvut.cz
Department of Computer Science,
Czech Technical
University,
Karlovo namesti; 13, 121
3D-Dithering is a special lossy method for voxel model compression. It is highly recommended, for medicinal data, because 3D-Dithering has very low level of degradation, and we can successfully apply another method to Undithered data.
Data compression, dithering, medicine data
As grow a technical level of computer technology, we can notice problem of processing and archiving very huge volume of electronic data. This problem has been solved by many scientists.
Now we can solve problem of very large volume of information by many of common (Huffman coding, LZW, LZArit etc. [1] ) or specialised (compression of images or some network compression methods) compression algorithms.
These trends we can see also in computer graphics, e. g. in processing of large voxel models. This work is alternative approach to the problem of voxel model compression.
Originally, Dithering has been developed for colour reduction in two dimensional pictures.
Dithering as a compression method is a problem, which we can use as for two dimensional pictures as for three dimensional voxel models. In the first step of explanation, I describe how we can use dithering for image compression [3].
Basic Principles of 2D-Dithering Compression Method we can summarise in four steps.
For a 2D-Dithering I used Floyd Steinberg Dithering, but it is possible to make some experiments with Ordered Dithering or similar method.
Floyd-Steinberg Dithering and 3D-Dithering have one important feature: precious error distribution.
If original voxel intensity is 
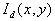
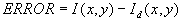
On the image is the one possibility of distribution of this error information.
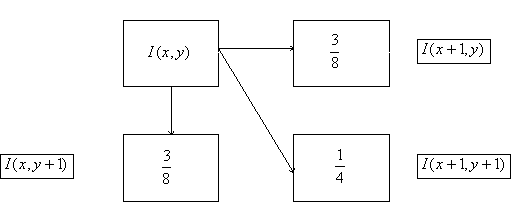
This possibility of error diffusion we can describe via this equations:
2D-Undithering is inverse process for Dithering. This Process we can implement using convolution [2], [3].
A
is convolutory matrix with size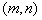 . But almost m and n
are odd integers. Undithered intensity
. But almost m and n
are odd integers. Undithered intensity 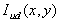 we
can describe from dithered intensity
we
can describe from dithered intensity 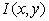 as:
as:
Matrix A is an normal convolutory matrix. With good result I used these matrixes:
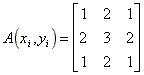
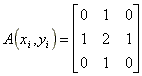


Basic Principles of 3D-Dithering Compression Method are very similar with two dimensional dithering, because it is only extension from 2D to 3D.

For 3D-Dithering is using an algorithm, which is very similar with Floyd-Steinberg Dithering. We can say, that 3D-Dithering is modified Floyd-Steinberg Dithering.
Floyd-Steinberg Dithering and 3D-Dithering have same feature: precious error distribution.
If original voxel intenzity is 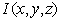

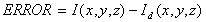

This possibility of error difusion we can describe via this equations:
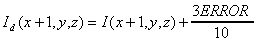
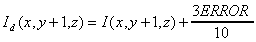
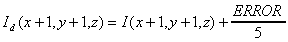
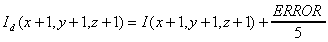
The most important thing of this method is, that error is distributed via diagonal and theoretically an error from first processed voxel change an intensity of last processed voxel. This feature minimalized a level of degradation an information at reduction intensity.
For good reconstruction of dithered information we can use one of the methods described below.
This method is not fully three dimensional, because it works only with two dimensional convolutory matrixes.
A
is convolution matrix with size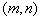 . But almost m
and n are odd integers. Undithered intensity
. But almost m
and n are odd integers. Undithered intensity 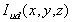 we
can describe from dithered intensity
we
can describe from dithered intensity 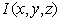 as:
as:
Matrix A is an normal convolution matrix. With good result I used this convolution matrixes:
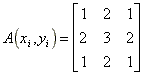
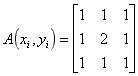
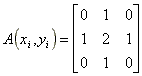


3D-UnDithering, method one is very poor method for making undithering in three dimensional space.
A
is matrix with size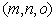 . But almost m
and n are odd integers and o is integer. Undithered
intensity
. But almost m
and n are odd integers and o is integer. Undithered
intensity 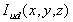 we can describe from dithered
intensity
we can describe from dithered
intensity 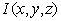 as:
as:
As convolution matrixes, we can use these matrixes:
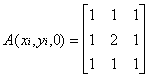
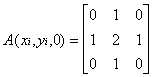
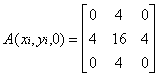
3D-UnDithering, method two is better than 3D-Undithering, method one. But this method is not adaptable, because this method uses only one convolutory matrix for all voxel model.

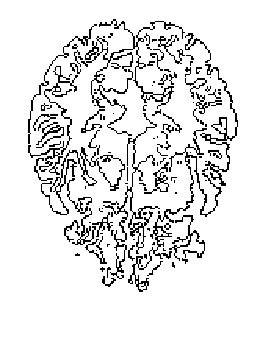
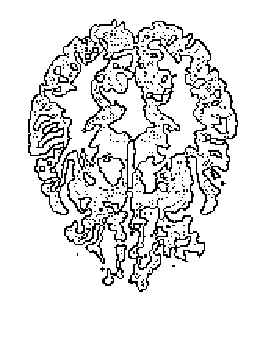
3D-Dithering, method one and two are not adaptable, because they use same convolutory matrix for all voxel model. This character makes high level of degradation.
For better quality we can use 3D-UnDithering with dynamic convolutory matrix. The most important thing of this method is, that we must compute origin convolutory matrix for each voxel.
This method will have these features:
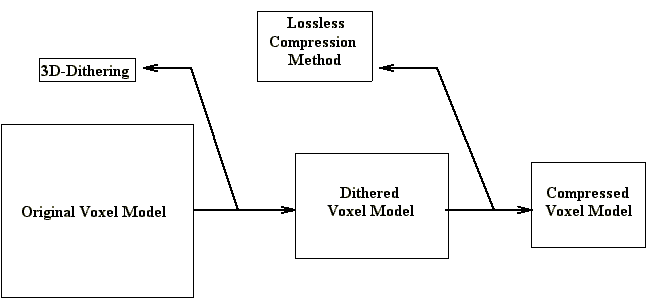
This method described has several aspect. It uses two compression steps: 3D-Dithering and lossless compression method. This approach has some features: after first decompression step, we can display voxel model (in low quality). This feature can make faster interactions via network connections.
[1] Melichar, B., Pokorny, J.: Data Compression, Report DC-92-04,Czech Technical University Prague, Department of Computer Science, 1992
[2] Stenger, A.:Converting Dithered Image Back to Gray Scale, Dr. Dobb's Journal, Nov. 1992, pp.64-68
[3] Slavik, P., Prikryl, J.: Dithering as a method for image data compression