 CESCG,
april 1997
CESCG,
april 1997 CESCG,
april 1997
CESCG,
april 1997
e-mail: medvid@virgo.dam.fmph.uniba.sk
This page created : Jaroslav Placek (translation) & Juraj Sofranko (HTML)
e-mail : 4Placek@st.fmph.uniba.sk;
4Sofranko@st.fmph.uniba.sk
Marshall Bern and David Eppstein, Mesh Generation and Optimal Triangulation, In: Computing in Euclidean Geometry, pp. 23-90, World Scientific 1992.
Jan Frykestig, Advancing Front Mesh Generation Techniques with Application to the Finite Element Method, Chalmers University of Technology, Göteborg, 1994.
Gabriela Bobáková, The Basic Data Structures of Computational Geometry and their Application in Language C and Pascal, Comenius University, Faculty of Mathematics and Physics, Bratislava, 1995. (in Slovak)
Many problems in engineering practice can only be solved on computers by the use of some numerical method, and in the engineering community the finite element method (FEM) is mostly used. Finite element methods have proved indispensable for physical simulation. These methods typically assume that the simulated domain - for example, the air around a wing - is divided into many small "elements", trinagles or quadrilaterals in two dimensions and tetrahedra or hexahedra in three ones. The complex of elements is the mesh. The purpose of the mesh is to provide the framework for the numerical solution of the engineering problem at hand. The decomposition of the domain into a mesh of elements is called mesh generation, and this, at first glance, seemingly simple problem is in fact so complex that it has limited the widespread use of the FEM.
A tringulation is a partition of a geometric input, typically the region defined by a point set or a polytop, into simplices that meet only shared faces. So in two dimensions, a triangulation consists of triangles that intersect only at shared edges and vertices. An optimal triangulation is one that is best according to some criterion that measures the size, shape, or number of simplices.
We discuss algorithms
for the optimization of triangulations on a fixed set of vertices
and briefly survey heuristic algorithms used in some practical
mesh generators.
Most numerical methods - there are exceptions - assume that the domain of interest is divided into a mesh of small, simple elements. There are two major types of meshes: structured and unstructured. This paper studies only unstructured meshes, but here we briefly sketch the larger context.
A structured mesh in two dimensions is most often simply a square grid deformed by some coordinate transformation. Each vertex of the mesh, except at the boundaries, has an isomorphic local neighborhood. In three dimensions, a structured mesh is usually a deformed cubical grid. An unstructured mesh is most often a triangulation with arbitrarily varying local neighborhoods.
Structured meshes offer certain advantages over unstructured. They are simpler, and also more convenient for use in the simpler finite difference methods. They require less computer memory, as their coordinates can be calculated, rather than explicitly stored. Finally, structured meshes offer more direct control over the sizes and shapes of elements.
The big disadvantage of a structured mesh is its lack of flexibility in fitting a domain with a complicated shape. A number of techniques have been developed to find appropriate coordinate transformations: conformal mapping, algebraic methods, and numerical methods that themselves solve differential equations. Even armed with these techniques, it may be impossible to find a transformation that fits a complicated domain acceptably well. Faced with this problem, some practitioners cut out a region of the grid, without any transformation, to give a "stair-case approximation" to the domain. But then the computed solution will be quite inaccurate near the boundary of the domain, an area that is often of special interest. Other practitioners break up the domain into simpler regions, perhaps overlapping, each of which can be more nearly matched by a deformed grid. This method and its associated numerical analysis make up "domain decomposition", a large area of study in its own right.
A finite element mesh
must use elements of appropriate size and shape, and these quantities
may vary over domain. Multiple requirements lead to many interesting
and difficult triangulation problems. These computational problems
and practical use of simulated annealing for solving this define
the subject of this paper.
The requirements for mesh
are similar to requirements of triangulation of geometric input.
For that reason except of finding correct mesh is replaced by
finding the triangulation. D-unit is convex hull of d+1
points in Euclidian space Rd, d2, which is not
included in any halfspace with dimension less than d.
Defínition 1. Let M = {pi | i=1, 2, ..., np} be a set of np points, np>d, from Euclidian space Ed, d2, with convex hull K. Then d-dimensional triangulation T = {ti | i=1, 2, ... nt} is a set of nt d-units, which fulfills folowing propertiesi:
Triangulation in three dimensions is called tetrahedralization (or sometimes tetrahedrization). A tetrahedralization is a partition of the input domain, point set or polyhedron, into a collection of tetrahedra, that meet only at shared faces (vertices, edges, or triangles). Tetrahedralization turns out to be significantly more complicated than triangulation. As in two dimensions, n represents the number of vertices of the input domain, and we distinguish several different types of domains.
In this section, we concentrate on existance and construction of tetrahedralizations, without concern for optimality. Existence and construction are already interesting, since many two-dimensional triangulation properties break down in three dimensions.
The first surprise is that different triangulations of the very same input may contain different numbers of tetrahedra. For example, choose n points vi=(i,i2,i3) on the moment curve. It is not hard to show that their convex hull can be triangulated with the C(n-2,2) tetrahedra of the form vivi+1vjvj+1. (In fact this is the Delaunay triangulation of these points.) A generalization of Euler's formula shows that any tetrahedralization of an n-vertex polyhedron has at most this many tetrahedra. If we choose the tetrahedralization carefully, however, we can achieve linear, rather than quadratic, complexity for the same input. In fact, any strictly convex polyhedron can be tetrahedralized with at most 2n-7 tetrahedra: choose a vertex v, triangulate each face of the polyhedron that is not adjacent to v, and then connect v to each triangle. This bound is within a factor of two of optimal, as any tetrahedralization of a simple polyhedron has at least n-3 tetrahedra.
Edelsbrunner, Preparata, and West in Tetrahedrizing point sets in three dimensions show how to construct a linear-complexity tetrahedralization of point sets. After tetrahedralizing the convex hull with only linear complexity as above, interior points are added one at a time. When a point is added, the tetrahedron containing it is replaced by four smaller tetrahedra.
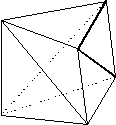 Figure
1 Schönhardt's polyhedron
Figure
1 Schönhardt's polyhedronWhen we try to extend these results to nonconvex polyhedra, we meet a second surprise: not all polyhedra are tetrahedralizable. Consider a triangular prism, and twist one triangle relative to the other so that each rectangular face of the prism folds into two triangles with a reflex edge between them (Figure 1). Any set of four vertices must include a pair that face each other across such a reflex edge. So the polyhedron contains no tetrahedron, and tetrahedralization is impossible.
This polyhedron, known as Schönhardt's polyhedron can be tetrahedralized if we add one Steiner point. This leads to the question of how many Steiner points may be required for tetrahedralization. Chazelle found a simple polyhedron in which (n2) Steiner points are needed even to partition the polyhedron into convex regions. Clearly, this is also a lower bound for tetrahedralization.
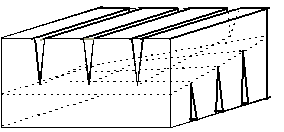
Chazelle's polyhedron
can be viewed as a cube, from which numerous thin wedges have
been removed. Wedges parallel to the y-axis are removed
from the top face of the cube, and wedges parallel to the x-axis
are removed from the bottom face. The reflex edges at the tips
of the wedges form two sets of lines, that almost meet at the
center of the polyhedron, near a ruled surface in the form of
a hyperbolic sheet (see Figure 2). Viewed from above, the lines
partition this sheet into (n2) small squares. Noncorresponding
points on any two squares are not visible to each other, and hence
must be in different convex regions. Therefore, (n2)
Steiner points are needed.
In this section, we consider three-dimensional optimal triangulation without Steiner points. Since Steiner points are required simply to tetrahedralize nonconvex polyhedra, this section treats only point sets (and as a special case, convex polyhedra). Even here very little is known, and this section has more open problems than results. Since a single input has tetrahedralizations of different complexity, a natural optimization question asks for a minimum-complexity tetrahedralization of a point set.
The Delaunay triangulation (DT) in three dimensions contains each tetrahedron with vertices from the input point set, whose circumsphere contains no other input points on its surface or in its interior. Assuming general position, in which no five points lie on a single sphere, so this defines a triangulation. The complexity of the DT may be as high as (n2), as shown by the moment curve example (Section Tetrahedralization without Optimization). There does not seem to be a reasonable definition of constrained DT in three dimensions.
We can use the lifting transformation. We map an input point with Cartesian coordinates (x,y,z) to the point (x,y,z,x2+y2+z2 ). The image points all lie on a paraboloid in four dimensions; the projection of the lower convex hull back onto the xyz-hyperplane gives the DT, as it is in DT in two dimensions. Coupled with an algorithm for computing four-dimensional convex hull, this gives a worst-case optimal, quadratic-time algorithm to compute the DT.
There are also direct algorhims. Bowyer and Watson gave incremental algorithms that are quite popular in practice. Watson's algorithm inserts points in sorted order by one coordinate, testing all old circumspheres that intersect the current sweep plane. Bowyer includes evidence that his algorithm runs in time O(n4/3) for a random point set.
Use of DT in 3D does not
grant well-shaped tetrahedras. As it is shown at the picture,
tetrahedron vertex can move on the sphere surface, so we get tetrahedron
with too small volume. This type of tetrahedron must be removed
from tetrahedralization. We replace it with tetrahedron got by
inserting of the new point or by moving the inner point in tetrahedralization.

Joe and Rajan generalized the flip algorithm for DT construction. In three dimensions, flips involve sets of five points, forming a tetrahedral bipyramid. Such a figure can be tetrahedralized in two ways: either as a pair of tetrahedra separated by a face, or as three tetrahedra surrounding an interior diagonal. Thus flips trade two tetrahedra for three, or vice versa. Starting from an arbitrary tetrahedralization, however, the flip algorithm can get stuck in a local optimum and fail to produce the DT.
Joe showed that, if we start with the DT of some point set, and add a single point (dividing the tetrahedron containing it into four, or if the new point is outside the convex hull, adding tetrahedra connecting it to the triangles it can see), then flipping from the resulting triangulation never gets stuck. All tetrahedra involved in flips are neighbors of the new vertex, so in some sense this flipping procedure becomes two- rather than three-dimensional. This result gives another O(n2)-time algorithm for computing the DT: add points one by one (say, in sorted order by x-coordinate) and, after each addition, flip until the DT is reached. Rajan described a similar procedure for incrementally adding points and flipping tetrahedra to find the DT. His procedure flips tetrahedra in the order corresponding to the changes in the convex hull of the lifted points as the new point is moved vertically down onto the paraboloid. Thus, Rajan's algorithm generalizes to higher-dimensional DT construction.
 Picture.9
Two ways for tetrahedralization of five points.
Picture.9
Two ways for tetrahedralization of five points.Because the DT posseses so many optimality properties in two dimensions, geometers long suspected that it should optimize something in three dimensions. Recently, Rajan discovered the first such result. (His result actually holds in all dimensions.) The min-containment sphere of a simplex t is the smallest sphere containing t. If t contains its circumcenter, then min-containment sphere circumscribes a lower-dimensional face of t. For example, in two dimensions, the min-containment sphere is either the circumcircle or the diameter circle of the longest edge.
Theorem. The Delaunay triangulation is the triangulation that minimizes the maximum radius of a min-containment sphere.
Proof Sketch:
Lift the points to the paraboloid (x,y,z,x2+y2+z2).
Any sphere corresponds to a hyperplane cutting this paraboloid.
Let be any triangulation, and for any tetrahedron t in , define
H(t) to be the half-space above the hyperplane corresponding to
the circumsphere of t. If S is the min-containment sphere
of t, the radius of S corresponds to the vertical distance
between the lifted center of S and H(t). Now form a polytope
P() as the intersection of all such halfspaces. (This can be thought
of as a power diagram in the original space.) Then the
largest min-containment sphere corresponds to the largest distance
between this polytope and the portion of the paraboloid to which
the convex hull of the input can be lifted. The DT is the convex
hull of the lifted points, so it is lower than any other possible
polytope P(), and hence minimizes this distance.
Most of the techniques for generating and improving two-dimensional meshes can be generalized to three dimensions, such as Octrees, Laplacian smoothing, Polyhedron decomposition, Advancing front, though not without some difficulties. Overall, three-dimensional unstructured mesh generation is still in its early stages of development.
Laplacian smoothing (when vertex v in the interior of the mesh is moved to the centroid of the polygon formed by its neighbors) generalizes to three dimensions but the improvement it offers may not be as significant as in two dimensions.
There are local transformations that trade two tetrahedra for three, and three tetrahedra for two, as it was discussed above. These transformations give the analog of the flip procedure in two dimensions, and may be used to improve a triangulation according to some criterion, such as the Delaunay empty circumsphere condition. In three dimensions, however, the flip procedure may get stuck in a local optimum that is not a global optimum. It is already known, that for the Delaunay criterion, special starting triangulations always lead to a global optimum.
The characterizing feature of the advancing front method is that nodes and elements are created simultaneously starting from the boundary of the domain of interest. In three dimensions, the initial front is created from the triangular facets of the boundary surface meshes. A triangle on the front is selected, and a tetrahedron is formed by placing a new node in a position so that the size of the tetrahedron satisfies the desired mesh size. Alternatively, an existing node is used if this results in a bettershaped tetrahedron. Following the construction of the tetrahedron, the front is updated in that facets no longer on the front are deleted and new facets are added. This procedure is repeated until the front is empty.
Algorithm of simulated annealing (ASA) is an algorithm for global optimization of very complex functions. This heuristic algorithm issues from process of annealing, crystallization of melt with very slow reducing of temperature to the point of gelation. The physical system is simulated by generation of random variety of atom configuration. The variety is acceptable, if it caused reduction of energetic level. Otherwise, the variety is accepted with particular expectation.
G. Bobáková used the ASA-method for the solution of the minimum weight triangulation problem. The desired algorithm for finding of the minimum weight triangulation consits in flipping triangulation edges to reduce the global sum of edge lengths. It can increase the global sum during annealing process. This is the way to find the global minimum of global sum. She achieved unusual results and tendered some hypothesis:
In this chapter I'll describe a method, which I used for generating the depth mesh
of point set in the space. This method uses simulated annealing algorithm. Initial triangulation is not randomized state but it is Delaunay triangulation created by "divide and conquer" algorithm. As we have shown, this classic triangulation in the space does not grant so much optimizing properties as it is in the plane. Exactly simulated annealing method would grant results which will approximate wanted properties of the mesh. This method is namely robust algorithm for searching global minimum of real function defined in the set Rn.
The goal of the method is to find optimal mesh, respectively mesh with properties mostly approximating initial user requierements. The mesh with lowest price with respect to price function will be understood as optimal mesh. Price function is weight sum of several purpose functions. In described method I aimed at creation of the mesh with lowest price, if price function evaluated tetrahedron curvature, total sum of mesh edges lenght and number of tetrahedrons. These criteria are important for threedimensional mesh creation. It is important for FEM(Finite Element Methods) that mesh cannot contain degenerated elements. Exactly disturbation criterion reveals these elements in the mesh.
Especially in 3D, the measure aspect ratio
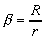
is the most often choice for disturbation measure of four-faced elements,
where R is a diameter of circumsphere of tetrahedron and r is a diameter of the smallest sphere embraced i