Texture of object surface represents a structure of surface. Any 2D texture we can represent by map:
t: Dt-->M, where Dt is subset of R2 and M is subset of R(R3).
Map t maps planar area (texture domain) to modulation space (gray-scale or true colors typically). Map t is often given by a table. The table is e.g. scanned picture or any other raster image.
In general, texture mapping is process which consist of:
.m: Dm-->Dt, where Dm is surface region.

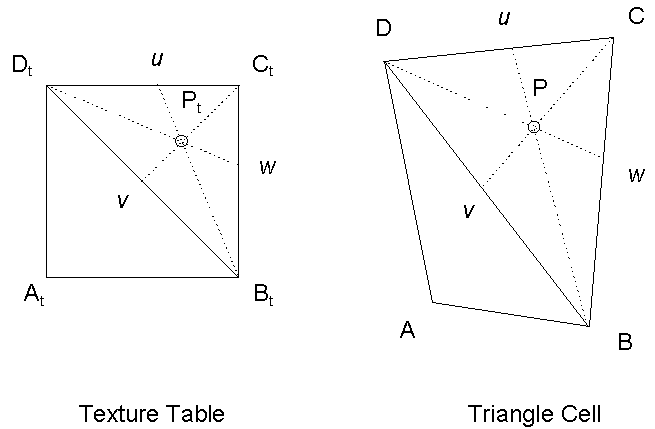
Figure 1: Inverse mapping in triangular mesh
In Figure 1 the inverse mapping of point P located in triangle BCD to matching texture triangle is demonstrated. Point P can be expressed as follows:
P = B + w (C - B) + v (D - B); u = 1 - v - w
(u, v, w) are barycentric coordinates of point P in triangle BCD. These coordinates can be obtained from the next formula:
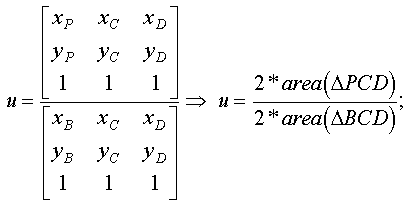
Formulae for remaining coordinates v, w could be derived analogously. Computing the double multiple triangle area costs 2 multiplication’s (MUL) and 4 subtraction’s (SUB).
2 * area(ABC) = (Ax - Bx) * (Ay - Cy) - (Ay - By) * (Ax - Cx)
The areas of mesh triangles could be calculated in pre-process. If area of some triangle is 0, the triangle should be excluded from mesh. Thus, it is possible to say, that each barycentric coordinate costs 2 MUL, 4 SUB and 1 DIV operations.
After obtaining barycentric coordinates (u, v), matching point in texture domain Pt can be expressed as follows:
Pt = Bt + w(Ct - Bt) + (Dt - Bt),
where Bt, Ct, Dt are texture coordinates corresponding to vertices B, C, D. Total sum of arithmetic operations necessary to obtain Pt is 8*MUL + 2*DIV + 12*SUB + 2*ADD. It's clear that algorithm based on just this approach can not be fast enough.
We would like to show disadvantages of inverse mapping if tetragonal mesh is used to warn developers to use it.
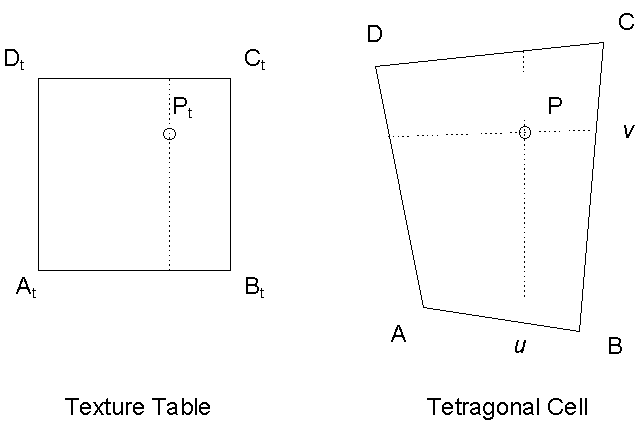
Figure 2: Inverse mapping in tetragonal mesh
There is possibility to consider that the tetragon ABCD in Figure 2 is bilinear patch. So for point P we can write:
P = (1 - v)[(1 - u)A + uB] + v[(1 - u)D + uC]
It is the system of two equations of type:
x = ax + bxu + cxv + dxuv,
y = ay + byu + cyv + dyuv,
where:
P = (x, y)
ax = Ax, ay = Ay
bx = Bx - Ax, by = By - Ay
cx = Dx - Ax, cy = Dy - Ay
dx = Ax - Bx - Dx + Cx , dy = Ay - By - Dy + Cy
To obtain (u, v) we can use the next formulas:
K = cxdy - cydx,
L = dxy - dyx + axdy - aydx + cxby - cybx,
M = bxy - byx + axby,
if K = 0, v = - M / L, else v = (- L - (L2 - 4KM)1/2) / (2K) and u = (x - ax - cxv) / (bx + dxv)
We are able to compute (u, v), but this computation costs too much processor time, because there are too many multiplications and also rather slow square root used. Since domain of square root is R+, it is necessary to distinguish whether tetragon is not degenerated to one line or non convex polygon. In case of degenerated rectangle we can not find solution always or we can not see some texture colors as it is shown in Figure 3. Bilinear transformation maps some texture coordinates outside the non convex tetragon ABCD. This fact excludes using tetragonal mesh which includes non convex tetragons, because result picture could contain fails (missing parts of texture)
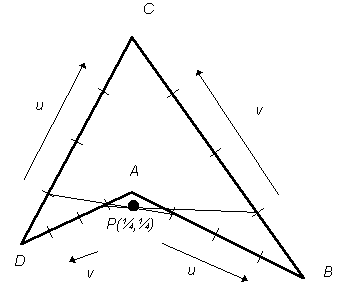
Figure 3: Bilinear interpolation of points of non convex tetragon
A tetragonal mesh is not often used in 3D space, because 3D tetragon is not planar in general. Slightly different situation could come to being if our work domain is 2D space (vector editor). Tetragons are planar and it seems that work with tetragonal mesh in plane is more natural than work with triangular mesh. This tendency is caused by fact that also textures used to be rectangular. We have made decision to implement interaction with rectangular mesh and texture mapping algorithm which works with converted triangular mesh. The conversion is hidden from designer. Since no vertex can be created by mesh conversion, triangles can inherit texture coordinates from tetragons.
This approach is good enough if the sample frequency (number of smallest elements able to have assigned color – pixels) of deformed mesh cell is similar to sample frequency of corresponding cell in texture "wallpaper". Example of a failure of this approach is shown in Figure 4 when mesh cell is sampled by quarter of texture sample frequency. The inverse map m maps each pixel in mesh cell to white texel.
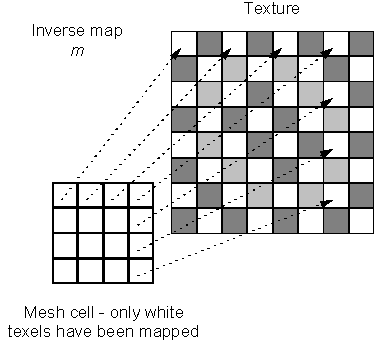
Figure 4: Failure of no color blending approach
The solution of previous problem is blending of texture colors around the matching texture coordinates. Sample frequency of matching texture part is higher than sample frequency of mesh cell in case of demonstrated failure. So, squared radius of neighbourhood sphere could be obtained as fraction a/b (one possibility), where a is number of texels in matching texture part corresponding to mesh cell and b is number of pixels in mesh cell. Number of texels or pixels respectively is given by cell areas approximately. Texels which are closer to matching texture coordinates than obtained radius, should be blended. The right image which is corresponding to example in Figure 4 should be light grey square approximately, because each pixel should be colored by color which is obtained by blending 2x2 texels (64/16 = 4 = 2x2). The example of color blending of 4 colors is shown in Figure 5.
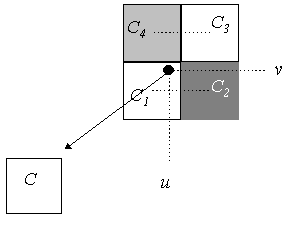
Figure 5: Bilinear color interpolation
C = (1 - v)[(1 - u)C1 + uC2] + v[(1 - u)C4 + uC3]
If sample frequency of mesh cell is higher, it could be sufficient just to take the color of matching texel or it is possible to enhance picture quality by bilinear interpolation of closest texel colors as is shown in Figure 5 and Figure 6
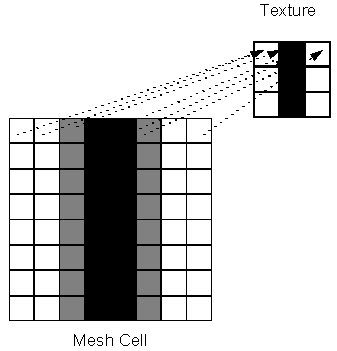
Figure 6: Enhancing the quality of
texture mapping,
if texture sample frequency is low