An Approach to Modeling Dirtiness
Dirtiness in the sense Becket and Badler use is: ‘any deterioration of some preconceived, idealized notion of perfection
corresponding visually to the result of human or natural processes’.
This approach's goal is not to create a model for imperfection using pure simulation of
particles or liquids, but using a rule-based system to create textures. The main reason
for this reduction of complexity is the fact that most imperfections are viewed from
distances where exact details of distribution or local appearance are indistinct.
Therefore any complete simulation of real world processed would mean enormous overcomputation.
But this simplification presents the major drawback of the approach, because using textures for modeling
dirtiness only works for blemishes that appear two-dimensional from standard human distances. Fortunately
these two dimensional imperfections comprise a large portion of our common notion of imperfection.
The whole approach involves two steps:
- Blemish instance modeling i.e. finding some technique to model a localized instance or concept of a blemish.
- Blemish placement i.e. designing rules that place or control distribution and local simulation of instances. This process constructs
relevant statistical parameters for local simulation given simple object information such as shape and composition and specific contextual
information such as the use of the object or location of adjoining objects.
Blemish instance modeling
Aside from Gaussian and random distribution functions, rule-guided aggregation and 2D
fractal subdivision are used to create the textures representing blemish instances.
Rule based aggregation can be used to construct tree like aggregates by simulating the
diffusion of randomly moving particles in a ‘sticky’ environment. Whereas one or more
particles are defined as sticky origins. During the diffusion simulation whenever a
particle collides with a sticky origin or a stuck particle there is a chance that particle
will also stick. If the moving particles are replaced by growth of the aggregation and the
sticking probability replaced by a growth probability based on any set of growth rules
considering such things as distance from the growth center and position of other particles,
interesting blemishes like rust and complex stains can appear (See Image 1).

Image 1. Rule-based aggregation (Rust)
In the late 80’s and beginning 90’s fractal has been ‘the Magic Word’.
Fractal methods were used - and sometimes misused - in virtually every scientific paper.
Therefore its not a big surprise that Becket and Badler include a fractal based approach for
creating textures in their paper.
2D fractal subdivision generate a 2D array of values which, when postprocessed and
interpreted appropriately, can achieve blemishes exhibiting fractal boundaries or
densities. The fractal dimension of the array can be
- interpreted directly as a mapping between two surface qualities.
- cut at a thresholding value to a binary map giving filled regions of circular Brownian motion.
- clipped to a range to form fractal Brownian motion rings (See Image 2).
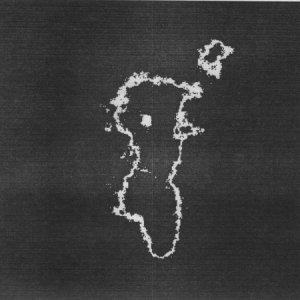
Image 2. Fractal (Coffee stain)
Blemish placement
After having discussed some techniques to model blemish instances the second step
concentrates on blemish placement.
Here are two examples:
- Scratches
Scratches are simple geometric primitives, just lines modifying surfaces either by
increasing the facet distribution value or revealing what is underneath a composite
surface. Scratches tend to appear oriented towards some dominant axis, sometimes due to
their actually occurring that way because abuse of an object is normally in the same
manner, and sometimes because scratch visibility tends to be anisotropic. A quick
approximation can exploit only the tendency for scratches to occur along a primary axis,
accomplished easily by writing lines of Gaussian-deviant orientation from the given
dominant axis. The intensities should then vary as a Gaussian of a given intensity.
- Splotches
Splotches of very viscous fluids or solutions such as tar or mud, after having hit a
surface, appear as several boundaried occurrences appearing to have fractal characteristics.
Modeling dried splotches is easily accomplished by interpreting a 2D normalized fractal
(see above).

Image 3. Planes in a room increasing from left to right in scratches and from top to bottom in
tar splotches.
Continue with Accessibility Shading.



