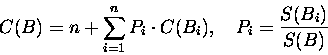Minimization of number of comparisons

We want to build a hierarchy, which will be used for fast searching. The structure we have chosen is a tree (not limited to binary). The leaves represent the initial bounding-boxes, internal nodes represent bounding-boxes that include their successors.

A distribution of probability for location of tested object is the same in the whole plane. Figure 1 shows a typical case.

 

Figure 1: Clustering two overlapping bounding-boxes into a bigger one

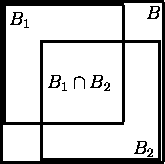
Presume the situation in the picture and that we should make a test in the extent of bounding-box B. At the beginning let's take only a binary tree. Then we have:

$P_1 = {{S(B_1-B_2)}\over{S(B)}}$	the probability, that we have to test the interior of bounding-box B1 which is outside B2.
$P_2 = {{S(B_2-B_1)} \over {S(B)}}$	the analogical case for the bounding-box B2
$P_3 = {{S(B_2 \cap B_1)}\over{S(B)}}$	the probability, that we have to test interior of both bounding-boxes B1 and B2
$P_4 = {{S(B-B_1-B_2)}\over{S(B)}}$	the probability, that we needn't test anything else

where S(B) is the area of the bounding-box B and total sum P₁+P₂+P₃+P₄=1.

The number of comparisons performed in the scope of bounding-box B is

$$C(B)=2+P_1\cdot C(B_1)+P_2\cdot C(B_2)+P_3\cdot (C(B_1)+C(B_2))$$

Number two in this equation means that we have to test both bounding-boxes B₁ and B₂ for intersection with the tested object. Then we may have to test the interior of one or both of them. For leaves of a tree (initial bounding-boxes) C(B)=0.

When many overlaps between bounding-boxes occur, the component $P_3\cdot (C(B_1)+C(B_2))$ has a high value and therefore we often have to pass both successors. This is worse than consecutive processing of bounding-boxes. We can solve this using a general tree, not only binary. Then we get a general expression:

$$C(B)=n+\sum_{i=1}^n P_i\cdot C(B_i) , \quad P_i={{S(B_i)}\over{S(B)}}$$

where n is number of successors for a given node B. In case of repeated overlapping we use sequential passing instead of inefficient tree (more comparisons in the scope of one node).