![\begin{figure}
\begin{center}
\begin{picture}
(160,80)(0,0)
\linethickness{0.5mm...
...\put(140,30){\framebox (20,20)[cc]{$B$ }}
\end{picture}\end{center}
\end{figure}](img10.gif) |
(Note: In fact the difference between the tree that we will get and the ideal tree depends just on the order and the selection of the first one, but we didn't solve this problem.)
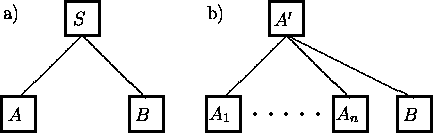
Let's have a tree of bounding boxes and one bounding-box (B) that we want to insert into the tree. (Starting with the root A). See the Fig. 2.
Than we have three possibilities how to do it:
 |
Now we will express the function C (which means number of comparisons) for each of the situations above.
| C1(S) | = | 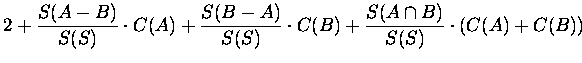 |
|
| C1(S) | = | 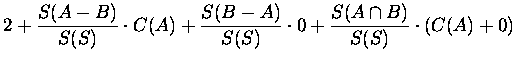 |
|
| C1(S) | = | 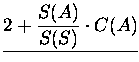 |
| C2(A') | = | 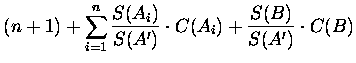 |
|
| C2(A') | = | 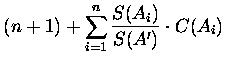 |
| C(A) | = | 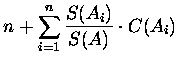 |
|
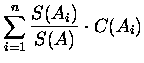 |
= | C(A)-n |
| C2(A') | = | 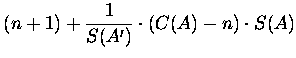 |
|
| C2(A') | = | 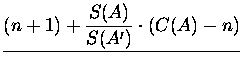 |
This means complete recursion. It seems like a big disadvantage that we have to parse the whole tree every time, but as the tree has complexity only O(n), it is not so significant.
The result from this situation is a value C3(A'), which is the lowest from all possible values for placing B inside A1 or A2,...,An.
In the end we'll choose that variant, which has the lowest value of C, it means the minimum number of comparisons.