Applications of Hardware-Accelerated Filtering


Ivan Viola
viola@cg.tuwien.ac.at


VRVis Research Center
Vienna / Austria
http://www.VRVis.at/vis/

Abstract

Software based filtering techniques often do not satisfy performance requirements of real-time applications. Therefore various hardware-based solutions have been introduced to the computer graphics community. In this paper we review methods that exploit the texture hardware features of consumer graphics cards for filtering purposes. We compare the texture-based filtering techniques to relevant existing solutions in qualitative and performance issues.

KEYWORDS: texture reconstruction, texture filtering, high-resolution filters, convolution filters, image processing, pattern recognition, graphics hardware.

Introduction

One of the fundamental tasks of computer graphics, image and signal processing is how to process the sampled data to get the desired result. The one-, two- and three-dimensional datasets are represented by discrete samples must fulfill certain conditions of sampling theory. Sampling theory is dealing with two fundamental tasks - sampling and reconstruction. Sampling describes how dense the original function should be sampled to be exactly described by its discrete representation. Reconstruction theory describes how to get the continuous function from its discrete samples [12]. The reconstruction process is defined as a convolution of the discrete sampled function with a reconstruction kernel. This kernel could be continuous, but in practice we also use discrete filters of high sampling resolution. The convolution sum between the sampled function and filter kernel is given by:

\begin{displaymath} g(x)=(f\ast{}h)(x) = \!\!\!\!\!\!\sum_{i=\lfloor x \rfloor -... ...}^{\lfloor x \rfloor + \lceil m \rceil}\!\!\!\!\!\!f[i]h(x-i), \end{displaymath}

where g(x) is the original function, f[i] its sampled representation and h(x) the reconstruction filter of width m. If the original function was band-limited before it was sampled we could perfectly reconstruct it using the sinc function as the filter kernel. The problem of the sinc filter that makes it unusable in practice is its infinite support.

Related work

Therefore several approaches have been introduced to perform high-quality reconstruction, based on approximation of the sinc on a limited interval. Keys [8] derived a family of cardinal splines suitable for reconstruction purposes, classifying the Catmull-Rom spline as numerically most accurate. Mitchell and Netravali [9] derived another category of cubic splines called BC-splines that are very popular as reconstructions kernel as well. They have classified various types of these splines according to the B and C parameters and determined boundaries of their admissible values. Theußl et al. [14] classified various windowing functions that limit the sinc extent to a particular interval, showing the Kaiser, Blackman and Gauss windows with best properties in the frequency domain. Möller et al. [10] presents a general framework for cardinal and BC-splines classification in spatial domain.

Although current graphics chips are equipped with a lot of features, the problem of the insufficient precision of the current hardware remains. Therefore, there are just few approaches to use the hardware for filtering. The methods are mostly dealing with image processing filtering methods such as the algorithm introduced by James [7]. This approach exploits the texture hardware for image processing convolution. The only method using hardware for high resolution filtering for reconstruction purposes is proposed by Hadwiger et al. [2,3,4]. This general framework for hardware-based filtering also exploits the texturing hardware the filtering purposes. The image processing convolution by James can be considered as a subset of this general framework.

Beside these methods another approach was proposed by Hopf and Ertl [5] using OpenGL Imaging Subset [11] and texture hardware to extend the natively supported 2D convolution to 3D. A year later they introduced non-linear hardware-accelerated image processing with erosion and dilation operators [6].
The reason why we do not use the OpenGL Imaging Subset is insufficient performance on consumer hardware, as well as the limitation to image processing tasks.

Hardware based filtering using textures

Graphics chips are designed to perform the primitive mathematical per-fragment operations for all fragments simultaneously. This fact is exploited in all texture-based filtering techniques [2,3,4,7]. These algorithms are based on the distribution principle used in splatting rendering solutions as well [15]. Instead of gathering all input sample contributions within the kernel width neighborhood of single input sample, hardware solutions use different evaluation order. This distributes all single output sample contributions to all relevant output samples. 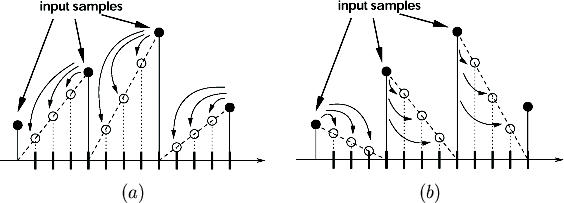We show the hardware based distribution filtering principle on a tent filter example. The input sample function is stored in one texture the filter kernel in another one. The kernel texture is scaled to cover exactly the contributing samples. The number of contributing samples is called kernel width. To be able to perform the same operation for all samples in one time, we have to divide the kernel into several parts to cover always only one input sample width. Lets call such parts filter tiles. The tent filter is of width two - there are two samples contributing on the output resampling points between them. Instead of taking the whole filter kernel, we take first the left tile of it. As already mentioned this is scaled exactly to the width between two input samples. To compute the ``left'' contribution of each input sample we shift the input texture to the left by one half of the sample distance. After this each input sample covers exactly the left tile of the filter kernel. Now we have the input function in one texture and the kernel tile of the input texel width in another one. The kernel texture is repeated to cover the whole input function. We set the numerical operation between these two textures to multiplication and render it to the framebuffer. This subresult is the left tile contribution of each input sample to the output resampling points. This is done in a single rendering pass. We repeat this process with the right tile, set the framebuffer blending function to addition and render the other contribution to the framebuffer again. Framebuffer stores the result of the filtering process that took two rendering passes. The distribution of the left and right tile contribution is illustrated in figure 1.

Figure 1: Distribution of left (a) and right (b) contributions on the resampling points.
\begin{figure*}\epsfysize =40mm \begin{displaymath} \begin{array}{cc} \epsffile{... ...s/left_hand_neighbor.eps}\\ (a) & (b) \end{array}\end{displaymath}\end{figure*}

Filtering algorithms

The general filtering algorithm uses two textures simultaneously. In the case when the hardware is able to use more than two textures in a single rendering pass, we can perform more filtering passes in one rendering pass. This increases the processing perfomance in some cases almost linearly and leads also to qualitatively better results due to exploiting the hardware internal precision for the addition as well. The precision of the framebuffer is 8 bits, while the internal precision of the best consumer cards of today is up to 12 bits. All the algorithms described below can be to expanded to take advantage of more available texture units or they can be combined together to achieve optimal results. Each algorithm has its own notation - the first three letters identify the filtering algorithm and the rest describe the number of used texture units within the rendering pass.

High resolution filtering vs. image processing

The filtering process discussed till now was a generalisation for all convolution based filtering methods. However in the special case of image processing filtering, where the input and output sample grid is exactly the same, we can use the James algorithm. Instead of using texture tiles for representing the filter kernel, we use color values. Image processing filters are very rough approximations of the continuous ones. They represent each part or tile only by one value, therefore we can substitute the filter texture with color values. The reason for using color values instead of textures is saving the texture traffic and number of texture units, which could be used to fold more filtering passes into a single rendering pass.
The ``dot'' algorithm can be used for image processing task as well, but the algorithms exploiting filter kernel properties are irrelevant, because the whole image procesing filter is stored in a lookup table in just a couple of float values.

Applications

This section reviews the possible application areas of the hardware based filtering approach. Firstly we are going to mention the high resolution filters applicability and then some image processing areas. The biggest importance of the hardware filtering principle is its generality - it is possbile to use any type of filter to achieve high-quality results in real-time.

Surface textures

The first application area of high resolution filtering is surface texturing. We use higher order filters of width four, namely cubic B-spline, Catmull-Rom spline and Kaiser windowed sinc of width four. Using such filters is especially effective, when the input texture is sampled at low frequency. Reconstructing it using hardware native linear reconstrucion results in visible artifacts. Software based higher order reconstruction would not have sufficient filtering performance. The typical low texture resolution representatives are lighting effects, such as lightmaps [1]. We show the results of various filter types in figure 2. The performance of the state-of-the-art graphics cards using various filtering algorithms is shown in the tables 1 and 2. The tested texture is of 64 x 64 resolution.

Table 1: Framerates of NVidia GeForce3 surface texturing, using different filtering algorithms. In brackets is the number of rendering passes.
# pixels std-2x (16) std-4x (8) dot-2x (4) dot-4x (2) sep-3x (16) spd-3x (4)
60k 55 105 190 275 55 190
180k 55 57 125 108 55 188
260k 50 36 80 60 46 150
900k 25 15 28 19 22 70
1200k 20 18 28 13 15 55



Table 2: Framerates of ATI Radeon 8500 surface texturing. In brackets is the number of rendering passes.
# pixels std-2x std-4x dot-2x dot-4x sep-3x sep-6x (8) spd-3x spd-6x (2)
60k 24 46 90 167 24 46 90 167
180k 24 34 71 78 24 46 71 83
260k 17 19 45 45 24 46 55 62
900k 9 9 20 19 23 35 26 27
1200k 8 9 16 15 16 24 55 32


Figure 2: Surface textured teapot using tent, cubic B-spline, Catmull-Rom spline and Kaiser windowed sinc filters (from left to right).
\begin{figure}\epsfysize =25mm \centerline{\epsffile{pics/surface_texture.eps}}\end{figure}

Solid textures

In this case we are dealing with the same higher order filters as in the 2D case, however they are three-dimensional. This texturing approach is used in cases, when the two-dimensional description does not provide acceptable results. Some examples are marble and wood materials. To be able to store more 3D textures in the hardware memory, we have to store them in low resolution. To obtain high-quality results from such datasets, higher order filtering must be performed. Another application area of growing importance is volume rendering. To avoid the linear reconstruction artifacts, the kernels of higher order are involved again. The tables 3 and 4 show the performance of various algorithms on a 128 x 128 x 128 dataset. This dataset is shown in figure 3 comparing tri-linear to tri-cubic interpolation.

Table 3: Framerates of NVidia GeForce3 solid texturing.
# pixels std-2x (64) std-4x (32) dot-2x (16) dot-4x (8) sep-4x (64) spd-4x (16)
60k 19 21 64 66 21 76
180k 6.5 6.8 20 20 14 50
260k 4.2 4.5 11 11 8.7 34



Table 4: Framerates of ATI Radeon 8500 solid texturing.
# pixels std-2x (64) std-4x (32) dot-2x (16) dot-4x (8) sep-4x (64) spd-4x (16)
60k 23 26 71 71 59 90
180k 4.2 4.5 15 16 30 30
260k 2.8 2.3 8 9 18 40


Figure 3: Solid textured teapot using tent and cubic B-spline filters (from left to right).
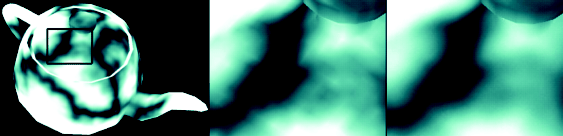\begin{figure}\epsfysize =30mm \centerline{\epsffile{pics/solid_texture.eps}}\end{figure}

Animated textures

High-quality reconstruction is even more important when using animated textures than in the static case. Linear interpolation produces much more visible artifacts, because the underlying interpolative grid, already stronly visible in the static case, appears as static layer beneath the moving texture. Higher order filtering like cubic interpolation completely removes such artifacts. This effect is most visible in animations with rotating objects. We divide the animation into the following three types according to their generation stage.

We show the difference between tri-linear and tri-cubic filtering on a pre-rendered animation frame of variable texture resolution in figure 4.

Figure 4: Prerendered animation frames from the space combat game Parsec [13] (top column) filtered with tent (middle) and cubic B-spline filter (bottom).
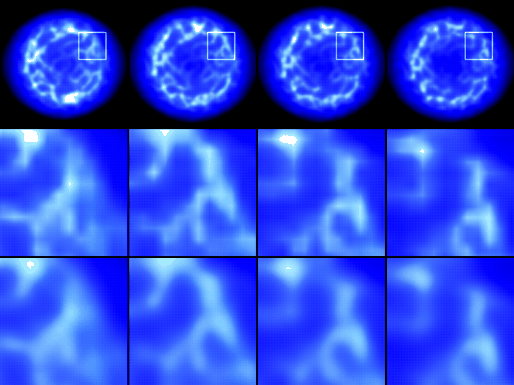\begin{figure}\epsfysize =85mm \centerline{\epsffile{pics/anim_parsec.eps}}\end{figure}

Derivative filtering

The previous applications used various function reconstruction filters. The generality of the filtering algorithm allows us to implement derivative reconstruction on hardware basis as well. This will make possible to compute, e.g., gradients on-the-fly, which are mostly computed in a preprocessing step in real-time applications. Although the simplest software solution - central differences - computes gradients in a short time, it produces visible staircase artifacts. This effect will be completely removed by using higher order high resolution kernels for the derivative reconstruction.

Smoothing

In our high resolution filtering implementation we have used filters of fixed width of four. The image processing filtering is extended to filters of arbitrary width. The typical filters of variable width are smoothing operators used for noise reduction in the way of cutting off the high frequencies of the image. We use two types of smoothing filters - averaging and Gaussian filter. The second one is based on the Gaussian lobe function that describes the noise distribution probability. The table 5 shows performance of the smoothing process on an image of 512 x 512 resolution. Filtering with kernels of width seven and higher results in strong visible summation artifacts. Therefore we are using quality improvement algorithms that provide acceptable results, but the framerates are about half of that from the benchmark table.

Table 5: Framerates of NVidia GeForce3 smoothing operation, using different filter kernel width.
kernel width img. subset std-1x std-2x std-4x dot-1x dot-2x dot-4x
3 3.26 120.00 180.00 185.00 275.00 307.00 314.00
5 2.86 50.00 74.00 75.50 118.00 169.00 155.00
7 2.48 28.00 40.50 41.70 90.00 131.15 121.00
9 1.95 17.00 25.50 26.40 50.00 73.66 76.45
11 - 12.00 17.55 17.99 41.48 61.30 55.96
13 - 8.20 12.61 13.55 26.86 41.75 43.15
15 - 6.24 10.03 10.05 22.39 36.68 35.40
17 - 5.00 7.66 7.96 16.76 28.17 25.27
19 - 3.95 6.30 6.61 15.02 23.42 24.12


Edge detection

The second type of image processing filters are edge detectors. These are applicable in almost all pattern recognition and computer vision areas, that involve almost always real-time performance. This is hard to achieve in software solutions, without exploiting any hardware. Our implementation uses two types of edge detector - Sobel and Laplacian operator. The Sobel filter approximates the first order derivatives and the Laplacian second order derivatives. The Laplacian filter uses only one convolution mask for the filtering process and is faster than Sobel. Its disadvantage is that it describes only the magnitude of the edge response. The Sobel filter consists of two or more kernels - for each dimension at least one. These filters are of more variations, the benchmark table 6 shows filtering performance on an image of 512 x 512 resolution for all of them. The Laplacian filter has two variations with low weight values and high. This has the impact on the resulting edge visibility. Similar to Laplacian, the Sobel filter is also presented with low and high weight values. The next Sobel clones use more than two filter kernels to improve the edge detection process. Also these are of acceptable performance. The results of the edge detectors using imaging subset and texture based filtering is shown in figure 5.

Table 6: Framerates of NVidia GeForce3 edge detection, using different edge detecting operators.
edge detector # kernels img. subset std-1x std-2x std-4x    
Laplace low 1 3.18 125.00 165.00 190.00    
Laplace high 1 3.18 77.00 118.00 120.00    
Sobel low 2 1.38 65.00 106.00 133.00    
Sobel high 2 1.38 66.50 97.00 94.50    
Sobel high 2 x 2 0.70 35.30 50.00 51.15    
Sobel high 4 x 2 0.35 16.91 23.30 24.10    


Figure 5: Edge detection using Laplacian low and high, Sobel low, high, high 2 x 2 and high 4 x 2 edge detector variations (from left to right). Upper image is filtered using OpenGL Imaging Subset and below is corresponding texture based filtering result. The resulting colors are inverted.
\begin{figure}\epsfysize =35mm \centerline{\epsffile{pics/edge_cescg.eps}}\end{figure}

Artistic rendering

Beside these fundamental convolution based operation, there are other arbitrary filters used in the desktop publishing area. We show that exploiting graphics hardware and combining various features, we are able to implement non-photorealistic rendering techniques at real-time performance. The artistic techniques discussed below are shown in figure 6.

Figure 6: Various artistic rendering techniques - painting with enhanced edges (a), filter combination on a pre-masked image (b), pointilism painting (c) and anisotropic filtering (d).
\begin{figure*}\epsfysize =30mm \begin{displaymath} \begin{array}{cc} \epsffile{... ...ffile{pics/artistic3.eps}\\ (c) & (d) \end{array}\end{displaymath}\end{figure*}

Post filtering

All the image processing filters mentioned above are possible to integrate in various applications. The idea of post filtering is to integrate such filtering directly into particular process that generates images, but instead of transferring them immediately to display, we process them with our image processing filters. This could be considered as ``screen space'' processing. The typical application is for example integrating non-photorealistic rendering technique in a standard renderer, or to filter the output from a CCD camera for video surveillance purposes. These examples are shown in figure 7.

Figure 7: Built-in real-time post filtering techniques.
\begin{figure}\epsfysize =35mm \centerline{\epsffile{pics/post_cescg.eps}}\end{figure}

Conclusions

We have presented a framework for texture based filtering with arbitrary filters. The framework shows possibilities to use higher order high resolution filter for reconstruction purposes, as well as simple image processing operators applicable in pattern recognition or computer vision. Exploiting graphics hardware makes possible to perform filtering tasks in real-time. The software implementations of such tasks are still far from real-time. We present an alternative to natively supported linear interepolation. To remove artifacts of linear filtering, we use higher order filtering techniques of real-time performance. The image processing operations can be performed at about 100 frames per second, which can strongly reduce the time consumption in, e.g., automatic person identification.

However, in some cases we still have problems with hardware shortcomings like framebuffer range and precision. The precision of 8 bits forces us to include quality improvement algorithms, that unnecessarily consume processing time.

Acknowledgements

This work has been done in the scope of the basic research on visualisation (http://www.VRVis.at/vis/) at the VRVis Research Center in Vienna, Austria (http://www.VRVis.at/), which is funded by an Austrian research program called Kplus.
Special thanks to Markus Hadwiger and Helwig Hauser for patient supervision.

Bibliography

1
M. Abrash.
Quake's lighting model.
In Graphics Programming Black Book. Coriolis Group Books, 2001.

2
M. Hadwiger, T. Theußl, H. Hauser, and E. Gröller.
Hardware-accelerated high-quality filtering of solid textures, technical sketch.
In SIGGRAPH 2001 Conference Abstracts and Applications, page 194, 2001.

3
M. Hadwiger, T. Theußl, H. Hauser, and E. Gröller.
Hardware-accelerated high-quality filtering on PC hardware.
In Proceedings of Vision, Modeling, and Visualization 2001, pages 105-112, 2001.

4
M. Hadwiger, I. Viola, and H. Hauser.
Fast convolution with high-resolution filters.
Technical Report TR-VRVis-2002-001, VRVis Research Center, Vienna, Austria, 2002.

5
M. Hopf and T. Ertl.
Accelerating 3D convolution using graphics hardware.
In IEEE Visualization '99, pages 471-474, San Francisco, 1999. IEEE.

6
M. Hopf and T. Ertl.
Accelerating morphological analysis with graphics hardware.
In Proceedings of Vision, Modeling, and Visualization 2000, pages 337-346, 2000.

7
G. James.
Operations for hardware-accelerated procedural texture animation.
In Game Programming Gems 2, pages 497-509. Charles River Media, 2001.

8
R. G. Keys.
Cubic convolution interpolation for digital image processing.
IEEE Trans. Acoustics, Speech, and Signal Processing, ASSP-29(6):1153-1160, 1981.

9
D. P. Mitchell and A. N. Netravali.
Reconstruction filters in computer graphics.
In Proceedings of SIGGRAPH '88, pages 221-228, 1988.

10
T. Möller, R. Machiraju, K. Mueller, and R. Yagel.
Evaluation and Design of Filters Using a Taylor Series Expansion.
IEEE Transactions on Visualization and Computer Graphics, 3(2), 1997.

11
OpenGL official site. http://www.opengl.org/.

12
A. V. Oppenheim and R. W. Schafer.
Digital Signal Processing.
Prentice Hall, Englewood Cliffs, 1975.

13
Parsec - there is no safe distance. http://www.parsec.org/.

14
T. Theußl, H. Hauser, and M.E. Gröller.
Mastering windows: Improving reconstruction.
In Proceedings of Visualization '00, 2000.

15
L. Westover.
Footprint evaluation for volume rendering.
Computer Graphics, 24(4):367-376, 1990.

About this document ...

This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.43)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -t 'Applications of Hardware-Accelerated Filtering' -antialias_text -antialias -white paper.tex

The translation was initiated by Ivan Viola on 2002-03-21

Ivan Viola 2002-03-21