

Next: A Flexible Framework
Up: Fundamentals of Volume Tracing
Previous: Participating media
In the course of implementing a volume tracing algorithm, it is necessary to
evaluate the integral equations for absorption, emission and scattering. The
problem is, that for all but the most trivial scenes, this can not be
done analytically. The only possible solution is to evaluate the
equations by means of numerical methods. The simplest numerical approximation
to an integral
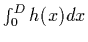 is the Riemann sum
is the Riemann sum
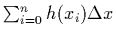 .
The interval
.
The interval ![$[0,D]$](img29.gif) is divided up into
is divided up into 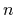 equal segments and for each
segment a sample
equal segments and for each
segment a sample 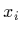 is choosen. The length of a segment is
is choosen. The length of a segment is 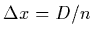 .
If shaded rendering is used, it has to be considered, that the sourceterm
.
If shaded rendering is used, it has to be considered, that the sourceterm 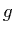 will also include a Riemann sum to approximate the absorption and emission
properties of the ``shadow feeler'' between the sample point and the
lightsource.
If the number of segments is chosen too low, aliasing effects may occur due to
undersampling of the underlying density functions. Undersampling will result
in striped images (similar to Mach-Bands) and loss of detail.
Participating media may also be incorporated into rendering systems using
global illumination, yielding some of the most impressive computer generated
images produced so far. Important work has been presented by Jensen
[JC98], [Jen96], as well
as Lafortune [LW96].
will also include a Riemann sum to approximate the absorption and emission
properties of the ``shadow feeler'' between the sample point and the
lightsource.
If the number of segments is chosen too low, aliasing effects may occur due to
undersampling of the underlying density functions. Undersampling will result
in striped images (similar to Mach-Bands) and loss of detail.
Participating media may also be incorporated into rendering systems using
global illumination, yielding some of the most impressive computer generated
images produced so far. Important work has been presented by Jensen
[JC98], [Jen96], as well
as Lafortune [LW96].


Next: A Flexible Framework
Up: Fundamentals of Volume Tracing
Previous: Participating media
2000-04-06