Fundamental balance statement

Continuous physical systems are mostly modelled using partial differential equations, and that also applies to flow and contaminant transport phenomena. Let us consider an infinitesimal volume, and formulate the law of mass conservation for it [1].

$$\frac{\partial\rho\Psi}{\partial t} = -\nabla\cdot(\rho\Psi v) - \nabla\cdot j + \rho f$$

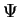$\Psi$ may be any balance quantity, in our case hydraulic potential 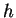$h$ or contaminant concentration 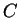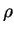$C$. $\rho$ is density, 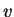$v$ is media velocity, 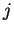$j$ is the mass flux and 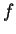$f$ covers any additional mass sinks or sources. The equation does mean nothing more than that the change of the mass within the volume equals the mass moving into it minus the mass moving out, modified by the yield of any internal source or sink. The actual mass fluxes can be calculated using famous laws of flow and transport.