Equations for groundwater flow

In the case of groundwater flow, the pressure differences drive water towards lower potential. We assume that the flow is slow enough to neglect inertial terms. Darcy's law describes exactly that situation[1].

$$\epsilon v = -\underline K(\nabla h - \Theta \xi)$$

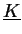$\underline K$ is the conductivity tensor, 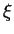$\xi$ is the direction of gravity and 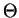$\Theta$ is a soil parameter called tortuosity. How much water is stored in the volume depends on the pressure there, as the liquid and solid material may both be compressed. Therefore, the change of mass depends on the change of pressure. The relation is described by the storativity 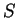$S$. Substituting those into the basic balance equation[1]:

$$L(h) = S\frac{\partial h}{\partial t} - \nabla\cdot(\underline K \cdot(\nabla h + \Theta \xi)) - \epsilon Q_{\rho} = 0$$

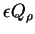$\epsilon Q_{\rho}$ represents additional sinks or sources.