

Next: The finite element method
Up: Modelling transport phenomena
Previous: Equations for groundwater flow
The case of pollutant transport is somewhat more complicated, as there are more phenomena to consider. The basic type of pollutant movement is advection, meaning that the pollutant moves along with the water.
Figure 1:
Transport Phenomena
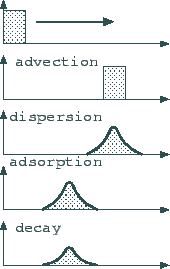 |
Molecular diffusion and macroscopic soil structure artifacts making the flow non-unidirectional cause that the pollution tends to expand in space. That is the phenomenon called dispersion. Adsorption means that the soil is able to gather pollutants, removing them from the solute. This is a two-way process, where the ratio of solved and adsorbed material depends on the concentration as defined by the sorption isoterms. The material removed form the solute is represented in the balance equation.
In addition, pollutants may decay as time passes. This happens both to solved and adsorbed material, however, the rate of decay in the two phases is significantly different, and the decay in the solid phase may be neglected, staying on the safe side. The final equation containing all factors of transport looks like[1]:
The first term stands for adsorption, the 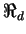 derivative retardation is similar to the storativity
derivative retardation is similar to the storativity 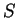 in the flow equation. The second term represents advection, the third is for dispersion, with
in the flow equation. The second term represents advection, the third is for dispersion, with 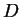 dispersion tensor calculated from molecular diffusion, longitudinal and transversal diffusion coefficients. The last two terms cover contaminant mass change from pollutant sources, polluted water entering or leaving the volume and decay, with decay coefficient
dispersion tensor calculated from molecular diffusion, longitudinal and transversal diffusion coefficients. The last two terms cover contaminant mass change from pollutant sources, polluted water entering or leaving the volume and decay, with decay coefficient 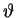 and solved material ratio
and solved material ratio 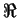 .
.


Next: The finite element method
Up: Modelling transport phenomena
Previous: Equations for groundwater flow
Szecsi Laszlo
2001-03-21
