

Next: Cube-Map
Up: Parameter Interpolation and Normalization
Previous: Parameter Interpolation and Normalization
The dot product between two vectors is only equivalent to the cosine of the
angle if the two vectors are unit vectors. So the two vectors
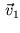 and
and
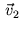 should be interpolated in a way that the interpolant
should be interpolated in a way that the interpolant
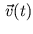 is moving uniformly between the two vectors and its length
remains one. As [14] point out this interpolations works on the
surface of the unit sphere and therefore it is called spherical
interpolation (Formula 3).
is moving uniformly between the two vectors and its length
remains one. As [14] point out this interpolations works on the
surface of the unit sphere and therefore it is called spherical
interpolation (Formula 3).
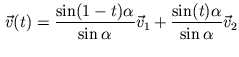 |
(3) |
Where
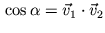 . Unfortunately spherical
interpolation is not available on current graphics accelerators, only
linear interpolation is supported. When using linear interpolation this
results in denormalized vectors (Figure 4) and
wrong shading intensities.
. Unfortunately spherical
interpolation is not available on current graphics accelerators, only
linear interpolation is supported. When using linear interpolation this
results in denormalized vectors (Figure 4) and
wrong shading intensities.
Figure 4:
Linear Interpolation versus Spherical Interpolation
|
|
Gerald Schröcker
2002-03-21
![]() and
and
![]() should be interpolated in a way that the interpolant
should be interpolated in a way that the interpolant
![]() is moving uniformly between the two vectors and its length
remains one. As [14] point out this interpolations works on the
surface of the unit sphere and therefore it is called spherical
interpolation (Formula 3).
is moving uniformly between the two vectors and its length
remains one. As [14] point out this interpolations works on the
surface of the unit sphere and therefore it is called spherical
interpolation (Formula 3).