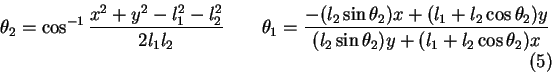Next: Iterative methods
Up: Solutions
Previous: Solutions
The algebraic solution of equation (2) exists only for a restricted
class of cases. The joint angles could be expressed using the end
effector position. The number of nonlinear equations increases with
the DOFs (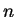 DOFs mean
DOFs mean 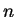 equations). Each joint angle -
one by one - could be solved by the system of
equations). Each joint angle -
one by one - could be solved by the system of 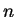 equations
[Chi96]:
equations
[Chi96]:
The 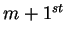 joint angle is expressed using the
joint angle is expressed using the 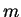 previous
angles. The last joint angle is expressed only by the end effector
position and orientation.
previous
angles. The last joint angle is expressed only by the end effector
position and orientation.
The forward kinematics solution
for the end effector position 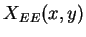 in 2 DOF structure
could be expressed as follows:
in 2 DOF structure
could be expressed as follows:
Thus, by applying elementary trigonometry the inverse solution is:
As the DOFs for most of cases are higher, the state vector is not
analytically expressible using such a trivial way. Therefore more
sophisticated approaches are necessary.
Lukas Barinka
2002-03-21
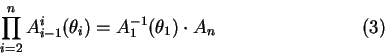
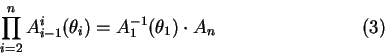
![]() in 2 DOF structure
could be expressed as follows:
in 2 DOF structure
could be expressed as follows: