


Next: Jacobian construction
Up: Iterative methods
Previous: Iterative methods
The Jacobian is the multidimensional extension to the differentiation
of a single variable [WW92]. As it was mentioned in the
introduction, there is a relation between the Cartesian space of the
end effector 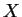 and the joint space of the joint angles
and the joint space of the joint angles 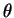 .
The Jacobian, in fact, transforms the differential angle changes to the
differential motions of the end effector [Mck91].
.
The Jacobian, in fact, transforms the differential angle changes to the
differential motions of the end effector [Mck91].
The vector 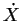 represents the linear velocity
represents the linear velocity 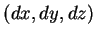 and rotational velocity
and rotational velocity
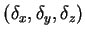 of the
end effector and
of the
end effector and 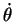 represents time derivative
of the state vector (rotational velocity for each joint).
represents time derivative
of the state vector (rotational velocity for each joint).
Since the unknown is 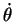 , the Jacobian inversion
is needed. Hence, the equation (6) is transformed to the form:
, the Jacobian inversion
is needed. Hence, the equation (6) is transformed to the form:
Lukas Barinka
2002-03-21
![]() , the Jacobian inversion
is needed. Hence, the equation (6) is transformed to the form:
, the Jacobian inversion
is needed. Hence, the equation (6) is transformed to the form: