| 
|
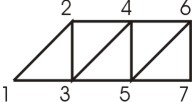
Figure 1:
The order of vertices to send is 1,2,3,4,5,6,7. |
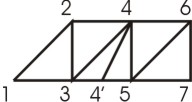
Figure 2:
The order of vertices to send is 1,2,3,4,4',swap/4,5,6,7. |
The triangle strip primitive is supported in many graphics libraries such as Irix-GL or OpenGL. In Fig. 1 a sequential triangle strip is shown. In this case each triangle is described by i th, (i + 1) st, and (i+2) nd vertices of the strip. Using the sequential strip, the transmit cost of n triangles can be reduced from 3n to n+2 vertices.
There also exists a situation where the triangle adjacency does not allow a sequential encoding. In Fig. 2 we have to break the strip, add an inverted edge 4',4 and continue with the rest of sequence. This inverting operation is called swap and strips using these swaps are called generalized strips.

| 
|
Figure 1:
The order of vertices to send is 1,2,3,4,5,6,7. |
Figure 2:
The order of vertices to send is 1,2,3,4,4',swap/4,5,6,7. |
The swap had been implemented as a one-bit attribute in GL. For better portability it was decided to not support it in OpenGL and one more vertex is sent to the engine instead. This means that an empty triangle appears. Although the swap costs one vertex, it is still cheaper to use the swap instead of starting a new triangle strip that costs two vertices.
Due to importance of this topic, many algorithms already exist. Because the computing of an optimal set of triangle strips is NP-complete [5], some heuristic is necessary. This means that each method has its own advantages and disadvantages. In this paper we want to explore and compare some of the existing algorithms. Using this knowledge, we want to develop our own stripification algorithm in the future.
There exist several different criteria of strip quality, such as number of strips, number of vertices, locality of the strip etc. The locality criteria are mainly useful if level-of-detail clipping of geometric models in complicated scenes is expected. As, at present, we solve only static visualization of simple scenes, we concentrated on number of strips and number of vertices criteria.
In Section 2, some of existing methods for non-hierarchical meshes are shown. In section 3, we describe the SGI based algorithms into more details [1]. Another OpenGL speed-up technique that can be combined with strips is presented in section 4. Experimental results are published in section 5. Conclusion and future work are discussed in section 6.