[Abstract] [Introduction]
[Configuration] [Optical
beacon tracking]
[Other issues] [Conclusions] [References]
We considered already many aspects of this issue. At the very beginning we had to solve the basic question of how to use the tracking data for our virtual-city fly-through and whether tracking data should include 3 or 6 degrees of freedom.
The shape of the stage was basically completely different than the "shape" of the virtual city model which was a square. A direct mapping of stage coordinates and model coordinates was not possible for two major reasons: i) the resolution of stage coordinates is much too small to allow mapping of these coordinates directly to a city model of about 100 by 100 houses and ii) the skater does not have any feedback of where she is currently moving (in the virtual city), i.e. for the skater there cannot be a direct connection between the things she does and the things she sees on the screen. So she can not control where to go in the city. This was a fundamental constraint from the beginning: the skater does not have to care about the city, she only does her performance.
In addition to these reasons mentioned we found also that skaters more or less run in circles, they cross the stage within a few seconds and change their running directions quite frequently. As a result of this, we accepted that a direct mapping of X- and Y-coordinates of the stage to fly-through camera coordinates is impossible.
To overcome this, we analysed the movements of inline figure-skaters to find out the most significant physical characteristics of a performance, which could be practicable for us. The most obvious things people observe during such a performance are spectacular things like pirouettes, somersaults and complicated jumps. As far as the skater's viewpoint is concerned, the physical quantity changing the most during these spectacular elements is probably the line of vision of the inline-skater. For example during a pirouette the skater turns about the z-axes, while performing a somersault she turns about an axis in the x-y-plane.
Besides the line of sight information some other properties are significant and interesting for our approach. During performance there were two figure-skaters on stage, a girl, whose cap was tracked and a man whose role was to guide the girl. The skaters change direction and stop quite frequently to do some figures. They raise speed to run in circles and reduce speed again to perform elements which are based on both skaters, i.e. they work together. For example the guy lifts up the girl, she "flies" around the guy, while he holds her stretched hands, or she is pulled through in-between his legs. These significant performance elements give rise to the consideration, that speed and height information can be used very well to characterise the movements physically.
But now we have been at the point to ask ourselves, what to do with these data values if they were available. Our conclusion was to use a predefined fly-through route and to adjust the position and orientation of the virtual camera according to the parameters mentioned above. The speed measure, which is calculated from subsequent (x,y)-positions of the skater, can be used directly as the speed of the fly-through. Also the height information can be mapped directly to the viewing process. During jumps on stage the skater was "virtually" jumping over the toy-houses on one hand, and reaching the virtual streets when bending down on the other hand. The only information, that was not available due to our tracking technique, i.e we used just one marker (see section 3), was orientation data. This unfortunately resulted in a decrease of "realism" observable for the audience, but with more ingenious algorithms and especially more time this could have been done as well.
To overcome the problem of lacking orientation data we thought of manually "inserting" some sort of orientation information, by using an operator who carries out appropriate actions for the different elements on stage, e.g. press a certain button if the inline-skater does a pirouette or a somersault. As we tried to manually insert "actions" this turned out to be just a pseudo solution which would confuse the audience more than it would help.
To round off, we more or less used a predefined fly-through route adjusting speed and height of the virtual camera by speed and "height" of a single marker, fixed onto the head of the inline-skater and tracked by two cameras.
As we decided to use a predefined fly-through "route" we had to provide some ways of establishing these routes interactively.
First of all we developed an interactive module to define the so-called "control-points" of the fly-through. These control points can be though of as points, which are similar to the control- or base-points of freeform-curves. Each control-point was determined by six values, the position vector containing the three coordinates x, y, and z, and the orientation vector containing yaw, pitch and roll respectively. These six values actually match exactly the 6 degrees of freedom in space. To define these control-points in a natural and convenient manner we used an input device called Space-Mouse. This device enabled us to move through the city adjusting all six parameters freely. To gain more accuracy we enabled the user to lock certain degrees of freedom, because it is somewhat difficult to control just a single degree of freedom with this input device. When trying to move forward one always moves slightly sideways and often alters pitch as well - one restriction of a Space-Mouse.
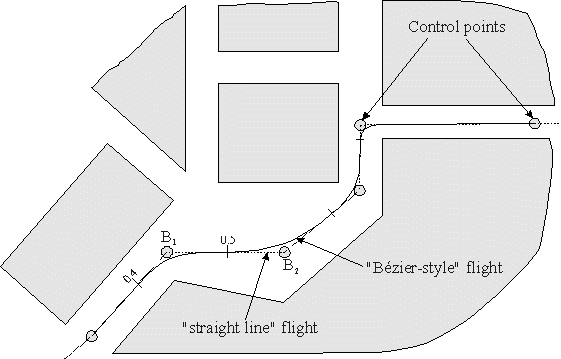
As soon as the control-points are established the user can decide whether to "fly" straight lines between these points or whether to smooth out the corners by flying round curves calculated as Bézier-curves. Figure 4 depicts a small part of a city as a bird's eye view and shows some control-points and the possible routes of flight between these points.

Figure 4: A part of a fly-through defined by control-points
For each control-point the user is able to adjust the position- and orientation data and to determine whether to fly straight lines or curves. In the latter case one additionally can determine the starting point of the Bézier curve by specifying a value in the range of 0.1 to 0.5. These are distance measures between adjacent control-points, e.g. for control-point B2 the distance measure 0.5 means that the starting point for the Bézier curve lies at half distance between B1 and B2.
A comfortable module based on Motif widgets was developed to define a fly-through route by means of a space-mouse. We also developed a data-format to store a fly-through route based on its control-points.
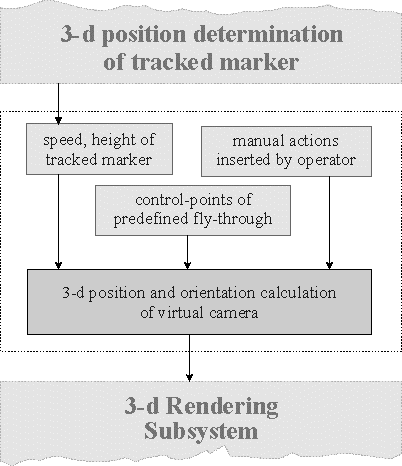
Figure 5: Block-diagram of position- and orientation calculation for virtual camera
Figure 5 is a more detailed depiction of the modules which contribute to the calculation of the final fly-through camera position and orientation. The top and bottom modules can be seen in figure 3 as well. As already mentioned in section 5.1 we enabled the operator to manually insert some actions which alter the orientation information.
The position and orientation of the virtual camera, which takes into account the speed and height of the tracked marker, the control points of the predefined fly-through route and possible manual actions of an operator is finally delivered to the rendering subsystem to visualise the virtual city at the right position and correct viewing orientation.
We developed a module which was capable of creating "realistic" city models of arbitrary size. Realistic is quoted because we didn't really use textures of real houses. We used houses ("toy-blocks") with two kinds of textures: simple ones (wooden or brick textures) or graffiti textures.
As already mentioned earlier, we had to create different "districts" in the virtual town which were consistent with the style of the inline-skate performance. So the fly-through started in a kind of dark and grey-styled district and moved on to some sort of fancy graffiti-styled part, as the performance becomes "freakier".
Previous Chapter |
Next Chapter |
Pages created and maintained by Stefan
Brantner
Last update: 15.04.1997
Institut for Computer Graphics and
Vision
Graz, University of Technology