In equation 15 the unknown function I appears on both
sides. Substituting the right side's I by
, which is obviously I according to the
equation, we get:
Repeating this step n times, the original equation can be expanded into a Neumann series:
If integral operator 
is contractive, that is if
then 
, thus
The contractive property of comes from the fact that
a reflection or refraction always decreases the energy.
The terms of this infinite Neumann series have intuitive meaning
as well: 
comes from the emission, 
comes from a single reflection, 
from two
reflections, etc.
In order to study the structure of 
, let us
consider the case of i=2:
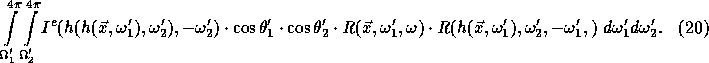
To evaluate the integrand at point 
, the following algorithm must be executed:
-- that is the point
which is visible from 
at direction 
-- must be
determined. This can be done by sending a ray from into
direction and indentifying the surface that is first
intersected.
-- that
is the point visible from 
at direction 
is
identified. This means the continuation of the ray tracing at
direction .
in the
direction of 
is acquired and is multiplied with the
cosine terms and the BRDFs of the two reflections.
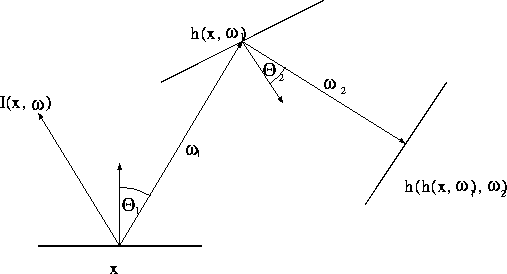
This algorithm can easily be generalised for arbitrary number of
reflections. In order to compute the contribution of the nth
reflection of the light to 
, the following
function should be integrated: A ray is emanated recursively
from at direction then from the found surface at
, etc. until 
. The emission intensity at the end of
the walk is read and multiplied by the BRDFs and the cosine
terms of the stages of the walk.
These walks provide the value of the integrand at ``point''
. The integral is
estimated as the average of these values.
Directions should be
selected to minimise the error of the approximation.
Thus we can conclude that the solution of the rendering equation requires the evaluation of high-dimensional ingegrals.