[CESCG logo] Reconstruction of Tomographic Data by Markov Random Fields

Marek Zimanyi


Department of Computer Graphics and Image Processing
Comenius University
Bratislava, Slovakia
 		[CESCG logo]

Traditional reconstructions and their defects

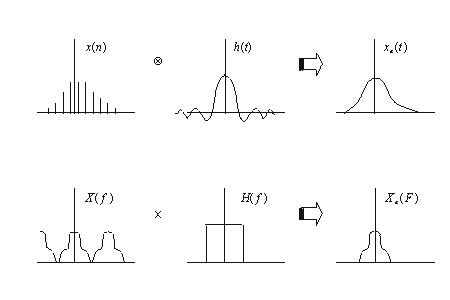
    Traditional reconstruction techniques are based on the convolution of interpolation filter with sampled data. The problem arises when the slices are scanned with big distances. This problem is formulated by Shanon ([WEIT], [PM]): Sampling interval T has to fulfill the relation  T < (1/2fmax), where 2fmax is the heightest Fourier spectral component in the sampled function and T = 1 / fs, sampling frequency fs is also called Nyquist rate.
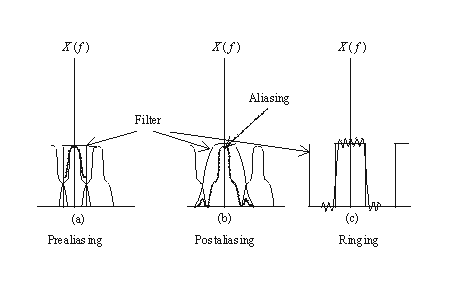
    Sampling a signal at a rate lower than postulated by Shannon leads to a very serious parasitic effect: aliasing (Figure1.).
    In our case (CT slices) aliasing appears because each slice is scanned with some radiation dose and high resolution CT data are usually taken only from cadavers. In MRI tomography, scanning a sufficient number of slices for 3D reconstruction requires medically unacceptable time.

Figure 1.
    The most commonly used interpolation is linear interpolation [PKT] or higher interpolation techniques based on convolution filter function with sampled data (Figure 2). However, results still suffer from staircase artifacts and false contours. A great interpolaton technique is shape based interpolation [HZB]. Although these techniques work well, removing the staircase artifacts, they can be used only for segmented objects and not for gray level tomographics.
Figure 2 (  Ä - conolution, ´ - multiplication).