Example

Conditions:

• random generated bounding boxes
• processing all pixels in raster as tested objects $(640\times 480)$

1.

Difference between values of function C and successive passing

See Table 1. and Figure 4.

n ... number of initial bounding-boxes

C_seq ... number of comparisons for successive passing (= n)

C_insert ... value of function C (number of comparisons) for the tree which was created with insert algorithm

$C_{insert}\over C_{seq}$ ... characteristic ratio in %

 

Table 1: Difference between values of function C

n	Cseq	Cinsert	$C_{insert}\over C_{seq}$
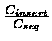2	2	1.05	52.5 %
5	5	1.71	34.2 %
10	10	3.96	39.6 %
20	20	6.71	33.5 %
50	50	9.55	19.1 %
100	100	15,22	15.2 %
200	200	20.43	10.2 %
500	500	33.43	6.9 %
1000	1000	51.15	5.1 %
2000	2000	78.10	3.9 %
5000	5000	149.02	3.0 %
10000	10000	254.64	2.5 %

 

Figure 4: Difference between values of function C

2.

Time complexity See Table 2. and Figure 5.

n ... number of initial bounding-boxes

t_seq ... time spended with successive passing

t_building ... time needed for building a tree with insert algorithm

t_searching ... time needed for searching within the created tree

t_insert=t_building+t_searching ... total sum for insert algorithm

... characteristic ratio in %

 

Table 2: Difference between time complexities

n	tseq[s]	tbuilding[s]	tsearching[s]	tinsert[s]
2	16	0	0	0	--
5	17	0	1	1	5.8%
10	18	0	2	2	11.1%
20	22	0	2	2	9.1%
50	31	0	3	3	9.8%
100	47	0	4	4	8.5%
200	80	1	5	6	7.5%
500	183	2	9	11	6.0%
1000	342	7	15	22	6.4%
2000	1242	27	22	49	3.9%
5000	--	160	45	205	--
10000	--	636	466	1102	--

 

Figure 5: Difference between time complexities

3.

Memory complexity - exactly linear, it means O(n)