|
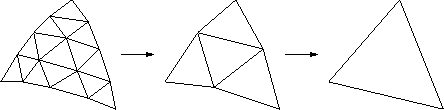
Wavelet-based algorithms do not explicitly manipulate the elements of the input mesh. Instead, its geometry is represented by multiresolution analysis in a more abstract way. You can think of this process as applying a low pass filter to the mesh creating a coarser mesh. At the same time, an high pass filter is used to capture the details (stored as wavelets) that are lost due to low pass filtering. This procedure can only be performed on meshes with subdivision connectivity (see figure
1). For more details on wavelets see [1].Only few meshes in practice satisfy the subdivision connectivity constraint. Therefore methods are required to transform arbitrary meshes to this special type. In [2] a solution is presented based on a discrete VORONOI-diagram. It is built upon the input mesh to separate it into triangular patches which are then remeshed with subdivision connectivity.