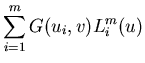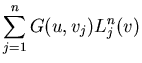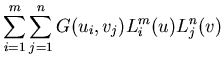

Next: B2-splines
Up: SPLINE - BLENDED SURFACES
Previous: SPLINE - BLENDED SURFACES
We are given a network of curves as mentioned above. It is desired to construct a surface
G(u,v) interpolating the given curves. Let us denote given u-curves
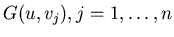 and v-curves
and v-curves
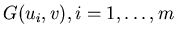 .
Curves intersect in points
.
Curves intersect in points
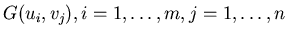 .
Gordon surface is defined:
.
Gordon surface is defined:
G(u,v)=G1(u,v)+G2(u,v)-G12(u,v)
where
| G1(u,v) |
= |
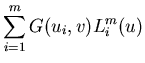 |
|
| G2(u,v) |
= |
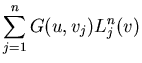 |
|
| G12(u,v) |
= |
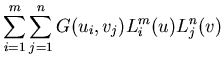 |
|
and Lim(u) are blending functions satisfying:
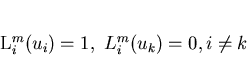 |
(1) |
We will use B2-splines to construct appropriate blending functions.
1999-04-09