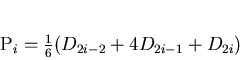

Next: Construction of blending functions
Up: SPLINE - BLENDED SURFACES
Previous: Gordon surface
B2-splajn is similar to B-spline. Instead of 2m+1 B-spline control vertexes
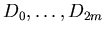 ,
B2-spline is determined by odd control vertexes
,
B2-spline is determined by odd control vertexes
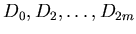 and even control points are replaced by points
and even control points are replaced by points
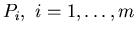 ,
joining segments Q2i-1 and Q2i. We will consider special case of
B2
-splines, when knot set is equidistant, in other words knot ui=i. In this case point
Pi holds an equation:
,
joining segments Q2i-1 and Q2i. We will consider special case of
B2
-splines, when knot set is equidistant, in other words knot ui=i. In this case point
Pi holds an equation:
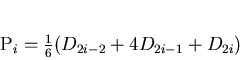 |
(2) |
To construct blending functions we need B2-spline functions. It is easy to derive
vertices of B2-spline function:
D2i=(i, d2i),
Pi=(i,pi). We do not
need to write first coordinate, so we will consider each control point to be identical to
its second coordinate. Next equations show, how we can count points of segments
Q2i-1 and Q2i:
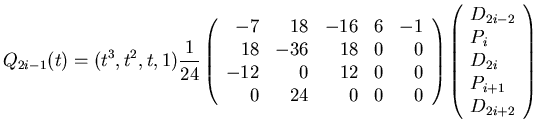 |
|
|
(3) |
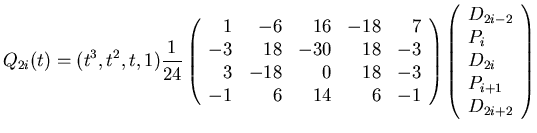 |
|
|
(4) |
where t=u-(2i-1) resp. t=u-2i.
1999-04-09