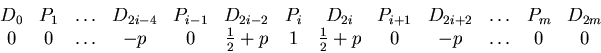

Next: Using blending functions to
Up: SPLINE - BLENDED SURFACES
Previous: B2-splines
In this section we will construct blending functions Lmi(u) as B2-splajn.
Let
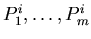 be joining points and let
be joining points and let
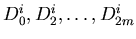 be odd control vertexes of blending function
Lmi(u). We have to change equation (1), because knot set is
be odd control vertexes of blending function
Lmi(u). We have to change equation (1), because knot set is
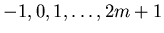 and one set of curves contains just m curves:
and one set of curves contains just m curves:
This is equivalent to conditions:
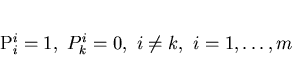 |
(5) |
Conditions (1) determine joining points
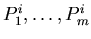 .
Odd control
vertexes do not need to satisfy any conditions. We have to find appropriate odd control vertexes.
Firstly we want the points of surface G1(u,v) to be a barycentric combination of points of
curves
.
Odd control
vertexes do not need to satisfy any conditions. We have to find appropriate odd control vertexes.
Firstly we want the points of surface G1(u,v) to be a barycentric combination of points of
curves
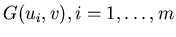 .
This is satisfied, if the next equation is satisfied:
.
This is satisfied, if the next equation is satisfied:
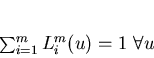 |
(6) |
We can thing about surfaces G2(u,v) and G12(u,v) in the same way.
We can easy get this conditions from equations (3), (4) and (6):
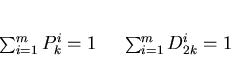 |
(7) |
Secondly, we want the given curves to influent the surface just locally. Therefore we want blending
function to be non-zero just over few segments around point Pii and knot 2i-1. The
optimal number of non-zero segments appears to be 12.
We can see from equations (3), (4), that segments Qi2j-1 and
Qi2j are controled by vertexes
Di2j-2,Pij,Di2j,Pij+1,
Di2j+2. If any of this two segments is identically equal to zero and
Pij=Pij+1
=0, then also
Di2j-2=Di2j=Di2j+2=0. If we have just 12 non-zero
segments, then just four odd control vertexes
Di2i-4,Di2i-2,Di2i,
Di2i+2 are non-zero. Obviously the only non-zero joining vertex is Pii=1.
Thirdly we want each given curve to have the same influence to Gordon surface. This will be satisfied,
if
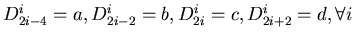 ,
where a,b,c,d are
real numbers.
Finally we want each blending function to be symmetrical. That means a=d and b=c. We did not
satisfy conditions (7) yet. First one is obviously satisfied. Now we can replace second
one by new simplier one: 2a+2b=1. Let p be a real parameter. We will set a=-p and
,
where a,b,c,d are
real numbers.
Finally we want each blending function to be symmetrical. That means a=d and b=c. We did not
satisfy conditions (7) yet. First one is obviously satisfied. Now we can replace second
one by new simplier one: 2a+2b=1. Let p be a real parameter. We will set a=-p and
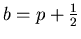 .
This is the result of construction. Now we can assume all verexes of
blending functions:
.
This is the result of construction. Now we can assume all verexes of
blending functions:
Now we need to note, that condition (6) for odd vertexes is not satisfied for
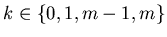 .
We need to increase the number of blending functions. We need also
Lm-1, Lm0, Lmm+1 and Lmm+2. In definition of
Gordon surface we can use for example
Lm-1+Lm0+Lm1 instead of
Lm1 and
Lmm+Lmm+1+Lmm+2 instead of Lmm.
.
We need to increase the number of blending functions. We need also
Lm-1, Lm0, Lmm+1 and Lmm+2. In definition of
Gordon surface we can use for example
Lm-1+Lm0+Lm1 instead of
Lm1 and
Lmm+Lmm+1+Lmm+2 instead of Lmm.


Next: Using blending functions to
Up: SPLINE - BLENDED SURFACES
Previous: B2-splines
1999-04-09