

Next: Computing points of curves
Up: SPLINE - BLENDED SURFACES
Previous: Construction of blending functions
In this section we will construct spline curve using blending functions. We are given m+3
control points
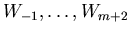 .
Spline curve L(u) is defined:
.
Spline curve L(u) is defined:
![\begin{displaymath}
L(u)=\sum_{i=0}^{m+1}W_{i}L^{m}_{i}(u), u\in [1,2m-1]
\end{displaymath}](img26.gif) |
(8) |
Curve L(u) interpolates control points
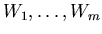 because of conditions
(5). Now we can count the B2-spline control points of the curve L(u).
Let us denote joining points of the curve
because of conditions
(5). Now we can count the B2-spline control points of the curve L(u).
Let us denote joining points of the curve
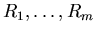 and odd control vertexes
and odd control vertexes
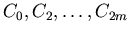 .
It is obvious that joining points are identical with control
points interpolated by the curve:
.
It is obvious that joining points are identical with control
points interpolated by the curve:
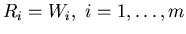 .
It is not difficult to count
the odd control points:
.
It is not difficult to count
the odd control points:
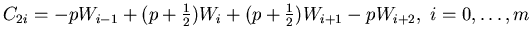 .
In simillar way we can get also approximating spline curve. We just need to replace condition
Ri=Wi by new one
.
In simillar way we can get also approximating spline curve. We just need to replace condition
Ri=Wi by new one
Ri=aWi-1+(1-2a)Wi+aWi+1
where a is real parameter. This will cause new values of joining points of blending functions:
Pii-1=a, Pii=1-2a, Pii+1=a. For a=0 we have got the original blending
functions. For 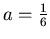 and p=0 we will get classical B-spline curve.
Implementation of spline curve is a good way to find out the best value of parameter p.
For interpolating curve it seems to be
and p=0 we will get classical B-spline curve.
Implementation of spline curve is a good way to find out the best value of parameter p.
For interpolating curve it seems to be 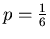 and for
and for 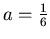 we will simply
choose B-spline value p=0. For other values of parameter a we can use linear interpolation
of this two values of p. We will get:
we will simply
choose B-spline value p=0. For other values of parameter a we can use linear interpolation
of this two values of p. We will get:
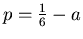 .
.


Next: Computing points of curves
Up: SPLINE - BLENDED SURFACES
Previous: Construction of blending functions
1999-04-09
![\begin{displaymath}
L(u)=\sum_{i=0}^{m+1}W_{i}L^{m}_{i}(u), u\in [1,2m-1]
\end{displaymath}](img26.gif)