If we want to represent rock wall only (including overhangs) we could generate height field that will not be in basic position. Instead we rotate this height field so that it will no longer represent function z=f(x,y) (for explanation of coordinates see above) but function x=f(y,z). Now we get a situation that we are able to represent slopes near vertical one, problem with horizontal slopes appeared. In real terrain orientation of surface does not vary chaotically, it is always possible to bound its part that can be represented with one of functions f(x,y), f(x,z) and f(y,z), so we can use for its representation appropriately oriented height field.
Collecting ideas from previous paragraphs we can formulate outlines of new data structure. We want different parts of terrain to be represented with rotated height field as well as hierarchy. It follows immediately that we can extend quadtree structure to octree, or structured grid in 2D into structured grid in 3D. Its elements will be either nothing (cell is void, its contents is air only), material (whole cell is filled with one material), rotated height field (height field defined above one of six faces of cell) or structured grid.
It is obvious that this data structure must be able to represent any ordinary height field regardless how fine the resolution of grid is. Except of continuity in x and y directions we must therefore solve the case that surface can go through several cells one above other. We can solve it in several ways.
The first one creates new type of cell contents---cell can contain besides height field also a reference to height field defined in another cell (this will be called forced height field). This means that in fact we ignore structure of the grid; things that can be represented with one height field are really represented in this way. It follows that problem of continuity in z direction disappears, modifications of this height field is easier than if the terrain is divided into several parts one above other. Nothing is for free, let us look at problems that arose. If one cell defines height field in +z orientation (it means ``common'' orientation, ie. height says how high is space filled with material in +z direction; this notation will be used throughout the rest of the paper), another cell above defines height field with -z orientation, then there is not obvious that these surfaces do not intersect. This would mean that one cell (in which intersection would appear) must have references to several height fields. This is nonsense both in physical sense and data structure, next it would not be possible to use simplified painter's algorithm for rendering. So if we want to avoid intersections we must check height fields somewhere in program. This checking would be quite difficult, remember that data structure is hierarchical---height field from the cell at some level in hierarchy can interfere in cells that are in hierarchy more above or more below. If we constrain this we get again the problem that was in the beginning, ie. continuity in z direction.
But there exists more serious problem. If we modify terrain not locally, ie. modification goes through several height fields (for example creation of river valley) we must know what height fields are connected to current one in x and y directions. If the reference to forced height field is represented with pointer to a cell that defines it, there is no information available where this cell lies in hierarchy, so we do not have information what height fields are connected. We can solve it either that in the cell with height field we store references to height fields this one is connected to (thanks to hierarchy there can be arbitrary number of such references) or to represent reference to cell like a path to that cell (thanks to hierarchy this path can be arbitrary long). In both cases we get a trouble with items of undefined length, this is quite a hard problem. We see that forced height fields bring more problems than they solve, so we must reject this approach.
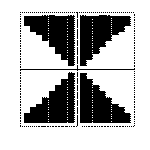
The second way of solving continuity problem is as follows. Height fields will not neighbour with cell faces, there will be a small margin. For rendering we must provide height fields as well as strips that fill these margins. Using this approach continuity problem would be solved in all directions, borders between cells would not be noticeable, there would be no software checking of continuity. The only thing that must be implemented is creation of these strips. Here we unfortunately get a problem that cannot be algorithmically solved. Even if we consider height fields in directions +z and -z only, there are cases that there is not clear how height fields should be connected. Example of this situation is at Figure 1. One of the presumptions was that there is no need for accurate description, but in sense of distances, not topology. For solving this problem we would (as in previous case) save topological information in cells. It can be seen that number of problems did not reduce. We must therefore reject this method and continue searching another alternative.

The third way of solving continuity problem must consider that the whole height field lies entirely in one cell and neighbours with its faces exactly. continuity of two height fields one above another can be solved with aligning---if a height overlaps borders of cell we clamp it into the appropriate interval. We can easily modify this idea so that two possible values in height field will denote ``height undefined''. The difference between them is that one height denotes ``here should be height below the cell'' and ``here should be height above the cell''. In this way we get in every cell height field that can have both on above and below a plateau. This does not matter on the side where this plateau will be covered with another height field; on the other side there must not be this plateau. It can be done so that renderer will obtain information both about height field and how to clip it (clipping planes)---most of renderers support this ability. Now height fields that lie one above another are exactly connected, it was done by modifying some distances. However, it was said several times that slight modification in distances does not matter too much. This approach saves topology. The problem here is a practical one: due to clamping of heights into appropriate interval some visible creases can appear on the borders of cells. These creases will respect grid structure, this is obviously undesirable.
With slight modification we can suppress this problem too. Modification comes from combination of ideas of clamping and forced height field. Height field in one cell could contain heights above and below the cell that would give information for better continuity. We can solve the situation so that we will not clamp heights that overlap cell borders. Nevertheless we give information about clipping planes to the renderer, so we have an illusion of forced height field but with well defined data structure. Of course, continuity of height fields must be checked in software, data on the cell borders will be redundant; this causes problems in every case. However there was not found better way how to achieve continuity.
In data structure there are another continuities than those described above. continuity between height fields of the same orientation ``on the sides'' (e.g. in x and y directions for height fields oriented +z) is trivial---it is sufficient to unify two appropriate heights. continuity between height fields of the same orientation ``above and below'' (e.g. in z direction for height fields oriented +z and -z) was described above. Problem is continuity of height fields of different orientation. Here it must be taken into consideration that heights are represented with finite precision, border of height field must be representable in both orientations and so on. Complete solution of these cases is still not entirely done. But it is necessary to know that in the worst case we can solve this by clamping even if the result is not perfect; it follows that problem has solution in this data structure.