

Next: Conclusions
Up: Index
Previous: Test Scenario
Results
In Fig. 3 the results of several gradient
reconstruction schemes of the sphere data set are depicted. In the
first row on the left the gradients were calculated analytically, in
the middle the central difference operator was used, which gave, and
that is quite interesting, for this data set the best looking
result. Surprisingly, the truncated cosc function (rectangular
windowed with width two, first row on the right) gives a really bad
result. Other windows with width two are better but not really
satisfying, as can be seen in Fig. 3 in the second
row. Only the Gauss windowed (with 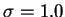 )
and the Blackman
windowed cosc function with window width three yield comparable
results to the central difference operator for this data set (depicted
in the third row left and middle image, for the right one a Lanczos
windowed cosc function of the same width was used which, admittedly,
shows some irregularities again).
)
and the Blackman
windowed cosc function with window width three yield comparable
results to the central difference operator for this data set (depicted
in the third row left and middle image, for the right one a Lanczos
windowed cosc function of the same width was used which, admittedly,
shows some irregularities again).
Figure 3:
Sphere data set. Gradients reconstructed analytically, with central differences and various windowed cosc filters with window width as depicted below the images.
| | |
![\includegraphics[width=4.8cm]{pics/sphere_analytic.ps}](img36.gif)
|
|
![\includegraphics[width=4.8cm]{pics/sphere_central_differences.ps}](img37.gif)
|
|
![\includegraphics[width=4.8cm]{pics/2_sphere_rect.ps}](img38.gif) width=2
width=2 |
|
| | | analytically |
| central differences |
| rectangular |
|
| | |
![\includegraphics[width=4.8cm]{pics/2_sphere_hamming.ps}](img39.gif) width=2
width=2 |
|
![\includegraphics[width=4.8cm]{pics/2_sphere_blackman.ps}](img40.gif) width=2
width=2 |
|
![\includegraphics[width=4.8cm]{pics/2_sphere_lanczos.ps}](img41.gif) width=2
width=2 |
|
| | | Hamming |
| Blackman |
| Lanczos |
|
| | |
![\includegraphics[width=4.8cm]{pics/3_sphere_gauss1_0.ps}](img42.gif) width=3
width=3 |
|
![\includegraphics[width=4.8cm]{pics/3_sphere_blackman.ps}](img43.gif) width=3
width=3 |
|
![\includegraphics[width=4.8cm]{pics/3_sphere_lanczos.ps}](img44.gif) width=3
width=3 |
|
| | | Gauss (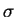 =1.0) =1.0) |
| Blackman |
| Lanczos |
|
|
Another test series was carried out with the Marschner Lobb test
signal. It can be seen, with analytically calculated gradients, in
Fig. 4 on the left. The images in the middle,
reconstructed with central differences, and on the right,
reconstructed with the derivative of the Catmull-Rom spline, show some
obvious irregularities.
Bounding the cosc function with windows of width two does not yield
much better results, as depicted in Fig. 5 first and
second row. Again, a simple truncation yields really bad results
(first row left image). Some windows show a slight improvement, but
the visual appearance of the central difference and, at any rate, the
Catmull-Rom spline derivative is still better. However, worth
mentioning is the adjustability of the Kaiser window with its
parameter 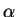 (as shown in the second row where the right picture
with
(as shown in the second row where the right picture
with 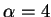 is much more appealing than the middle one with
is much more appealing than the middle one with
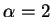 ).
).
Extending the window width to three, eventually, yields quite
satisfying results (Fig. 5 third and fourth row). The
two images in the middle column (Blackman window in the third and Kaiser
window with 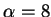 in the fourth) are, at last, quite smooth and
visually appealing. However, the left column shows images with
conspicuous artifacts due to the discontinuities at the edges of the
Hamming and Kaiser (with
in the fourth) are, at last, quite smooth and
visually appealing. However, the left column shows images with
conspicuous artifacts due to the discontinuities at the edges of the
Hamming and Kaiser (with 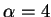 )
window. The right column shows
that also windows of width three can yield quite bad results. Notable
again is the adjustability of the Kaiser window, which ranges from
really bad (with
)
window. The right column shows
that also windows of width three can yield quite bad results. Notable
again is the adjustability of the Kaiser window, which ranges from
really bad (with 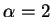 ,
third row right image) over getting better
(with
,
third row right image) over getting better
(with 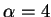 ,
fourth row left image) to really good (with
,
fourth row left image) to really good (with 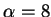 ),
and it gets worse again with an
),
and it gets worse again with an 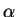 too high (for instance,
too high (for instance,
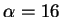 in the bottom right image).
in the bottom right image).
Figure 5:
Marschner Lobb data set. Gradients reconstructed with various windowed cosc function with window width as denoted in the lower right corners.
| | |
![\includegraphics[width=4.8cm]{pics/2_rect.ps}](img48.gif) width=2
width=2 |
|
![\includegraphics[width=4.8cm]{pics/2_welch.ps}](img49.gif) width=2
width=2 |
|
![\includegraphics[width=4.8cm]{pics/2_hamming.ps}](img50.gif) width=2
width=2 |
|
| | | rectangular |
| Welch |
| Hamming |
|
| | |
![\includegraphics[width=4.8cm]{pics/2_blackman.ps}](img51.gif) width=2
width=2 |
|
![\includegraphics[width=4.8cm]{pics/2_kaiser2.ps}](img52.gif) width=2
width=2 |
|
![\includegraphics[width=4.8cm]{pics/2_kaiser4.ps}](img53.gif) width=2
width=2 |
|
| | | Blackman |
| Kaiser (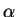 =2) =2) |
| Kaiser (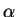 =4) =4) |
|
| | |
![\includegraphics[width=4.8cm]{pics/3_hamming.ps}](img54.gif) width=3
width=3 |
|
![\includegraphics[width=4.8cm]{pics/3_blackman.ps}](img55.gif) width=3
width=3 |
|
![\includegraphics[width=4.8cm]{pics/3_kaiser2.ps}](img56.gif) width=3
width=3 |
|
| | | Hamming |
| Blackman |
| Kaiser (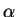 =2) =2) |
|
| | |
![\includegraphics[width=4.8cm]{pics/3_kaiser4.ps}](img57.gif) width=3
width=3 |
|
![\includegraphics[width=4.8cm]{pics/3_kaiser8.ps}](img58.gif) width=3
width=3 |
|
![\includegraphics[width=4.8cm]{pics/3_kaiser16.ps}](img59.gif) width=3
width=3 |
|
| | | Kaiser (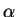 =4) =4) |
| Kaiser (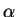 =8) =8) |
| Kaiser (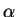 =16) =16) |
|
|
Further extending the window width yields, not very surprisingly, even
better results, however, just with certain
windows. Fig. 6 (on the top left) shows that, for
instance, the Bartlett windowed cosc function even with width four is
quite a bad choice and the Lanczos window (top right), although much
better, still shows some artifacts. Really good results, on the other
hand, were obtained by use of the Blackman window (first row, middle
image) which had quite a good result with width three already
(Fig. 5 middle image on the top). Also, the Gaussian
window gets now interesting, in the second row images obtained by
varying 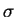 are depicted and at least the one with
are depicted and at least the one with 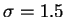 is quite good. The third row, again, shows the usefulness of the
Kaiser window by varying its parameter
is quite good. The third row, again, shows the usefulness of the
Kaiser window by varying its parameter 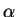 .
.
Figure 6:
Marschner Lobb data set. Gradients reconstructed with various windowed cosc functions with window width four.
| | |
![\includegraphics[width=4.8cm]{pics/4_bartlett.ps}](img60.gif) width=4
width=4 |
|
![\includegraphics[width=4.8cm]{pics/4_blackman.ps}](img61.gif) width=4
width=4 |
|
![\includegraphics[width=4.8cm]{pics/4_lanczos.ps}](img62.gif) width=4
width=4 |
|
| | | Bartlett |
| Blackman |
| Lanczos |
|
| | |
![\includegraphics[width=4.8cm]{pics/4_gauss1_0.ps}](img63.gif) width=4
width=4 |
|
![\includegraphics[width=4.8cm]{pics/4_gauss1_5.ps}](img64.gif) width=4
width=4 |
|
![\includegraphics[width=4.8cm]{pics/4_gauss1_8.ps}](img65.gif) width=4
width=4 |
|
| | | Gauss (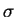 =1.0) =1.0) |
| Gauss (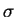 =1.5) =1.5) |
| Gauss (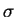 =1.8) =1.8) |
|
| | |
![\includegraphics[width=4.8cm]{pics/4_kaiser4.ps}](img66.gif) width=4
width=4 |
|
![\includegraphics[width=4.8cm]{pics/4_kaiser8.ps}](img67.gif) width=4
width=4 |
|
![\includegraphics[width=4.8cm]{pics/4_kaiser16.ps}](img68.gif) width=4
width=4 |
|
| | | Kaiser (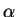 =4) =4) |
| Kaiser (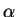 =8) =8) |
| Kaiser (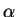 =16) =16) |
|
|


Next: Conclusions
Up: Index
Previous: Test Scenario
1999-04-08
![]() (as shown in the second row where the right picture
with
(as shown in the second row where the right picture
with ![]() is much more appealing than the middle one with
is much more appealing than the middle one with
![]() ).
).
![]() in the fourth) are, at last, quite smooth and
visually appealing. However, the left column shows images with
conspicuous artifacts due to the discontinuities at the edges of the
Hamming and Kaiser (with
in the fourth) are, at last, quite smooth and
visually appealing. However, the left column shows images with
conspicuous artifacts due to the discontinuities at the edges of the
Hamming and Kaiser (with ![]() )
window. The right column shows
that also windows of width three can yield quite bad results. Notable
again is the adjustability of the Kaiser window, which ranges from
really bad (with
)
window. The right column shows
that also windows of width three can yield quite bad results. Notable
again is the adjustability of the Kaiser window, which ranges from
really bad (with ![]() ,
third row right image) over getting better
(with
,
third row right image) over getting better
(with ![]() ,
fourth row left image) to really good (with
,
fourth row left image) to really good (with ![]() ),
and it gets worse again with an
),
and it gets worse again with an ![]() too high (for instance,
too high (for instance,
![]() in the bottom right image).
in the bottom right image).
![]() are depicted and at least the one with
are depicted and at least the one with ![]() is quite good. The third row, again, shows the usefulness of the
Kaiser window by varying its parameter
is quite good. The third row, again, shows the usefulness of the
Kaiser window by varying its parameter ![]() .
.