
Next: Bartlett Window
Up: Window Definitions
Previous: Window Definitions
The simplest method to bound the ideal derivative reconstruction
filter to some finite extend is to truncate it. This is tantamount to
multiplying it with a rectangular function which is 1 inside some
extend and 0 outside.
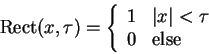 |
(5) |
Although the frequency response approximates the ideal one quite good
below 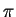 ,
it is significantly different from zero in form of bumps
above, which is due to the truncation and particularly annoying in
gradient reconstruction because it introduces artifacts even more
perceivable than in function reconstruction. To avoid these bumps,
other windows trade them against the rather good approximation below
,
it is significantly different from zero in form of bumps
above, which is due to the truncation and particularly annoying in
gradient reconstruction because it introduces artifacts even more
perceivable than in function reconstruction. To avoid these bumps,
other windows trade them against the rather good approximation below
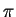 .
.
1999-04-08