

Next: Rectangular Window
Up: Index
Previous: Related Work
Window Definitions
In the following, definitions of some windowing functions are
given. All of the windows, except one, the Parzen Window
(Section 3.4), can be of arbitrary extend which is
specified by a parameter 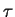 .
Fig. 2 on the left
depicts all windows with width two. Also all frequency responses
(Fig. 2 on the right) were generated (using the
discrete Fourier transform) with windows of extend two. Consequently,
we can directly compare the various windowed cosc filters with cubic
spline derivatives which have the same extend (the frequency response
of the derivative of the Catmull-Rom spline is depicted in
Fig. 1).
.
Fig. 2 on the left
depicts all windows with width two. Also all frequency responses
(Fig. 2 on the right) were generated (using the
discrete Fourier transform) with windows of extend two. Consequently,
we can directly compare the various windowed cosc filters with cubic
spline derivatives which have the same extend (the frequency response
of the derivative of the Catmull-Rom spline is depicted in
Fig. 1).
1999-04-08
![\includegraphics[angle=-90,width=7.2cm]{pics/polynomial_wins2.ps}](img13.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/polynomial_wins2_freq.ps}](img14.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/trigonometric_wins2.ps}](img15.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/trigonometric_wins2_freq.ps}](img16.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/gauss2.ps}](img17.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/gauss2_freq.ps}](img18.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/kaiser.ps}](img19.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/kaiser_freq.ps}](img20.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/polynomial_wins2.ps}](img13.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/polynomial_wins2_freq.ps}](img14.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/trigonometric_wins2.ps}](img15.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/trigonometric_wins2_freq.ps}](img16.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/gauss2.ps}](img17.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/gauss2_freq.ps}](img18.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/kaiser.ps}](img19.gif)
![\includegraphics[angle=-90,width=7.2cm]{pics/kaiser_freq.ps}](img20.gif)