| gx | = | 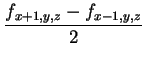 |
|
| gy | = | 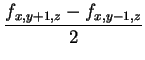 |
(4) |
| gz | = | 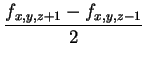 |
The most widely used method for gradient estimation is still the
central difference operator which simply computes an averaged
difference of values along each axes:
Bentum et al. [1] therefore proposed to use derivatives of cubic splines (which already were quite popular for function reconstruction [10]) as derivative reconstruction filters and Möller et al. [11,13,14] provide an analysis and analytic comparison of their performances. Machiraju and Yagel [8] discuss different gradient estimation schemes such as first reconstructing the function and then differentiating it or first differentiating the filter and convolving the data with that filter. An elaborated comparison is again given by Möller et al. [12].
Windowing itself is not that popular in computer graphics. Turkowski [19] used a Lanczos windowed sinc-function for decimation and interpolation of 2D image data. Goss [4] eventually proposed to use a Kaiser windowed cosc function for gradient estimation. This method will be more closely examined in Section 3.9.