
Next: Test Scenario
Up: Window Definitions
Previous: Gaussian Window
Kaiser Window
The Kaiser window [6] has an adjustable
parameter 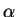 which controls how quickly it approaches zero at
the edges. It is defined by
which controls how quickly it approaches zero at
the edges. It is defined by
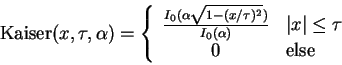 |
(13) |
where I0(x) is the
zeroth order modified Bessel function (for a
definition, and a more detailed discussion, of the Bessel functions
see, for instance, the Numerical Recipes in C [17]. The higher 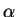 the narrower gets the window and therefore, due to the not so severe
truncation then, the less severe are the bumps above
the narrower gets the window and therefore, due to the not so severe
truncation then, the less severe are the bumps above 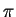 .
In Fig. 2 again, but in the
fourth row, several Kaiser windows are depicted with different values
for
.
In Fig. 2 again, but in the
fourth row, several Kaiser windows are depicted with different values
for 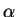 . The frequency responses on the right
shows that the parameter
. The frequency responses on the right
shows that the parameter 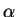 directly controls its
shape.
directly controls its
shape.
Goss [4] used this window to obtain an adjustable
gradient filter, but he used it only on sample points so that,
in between sample points, some kind of interpolation has to be
performed, which he does not state explicitly. In this work, the
Kaiser windowed cosc function will be used to reconstruct gradients at
arbitrary positions which is, of course, more costly.


Next: Test Scenario
Up: Window Definitions
Previous: Gaussian Window
1999-04-08