
Next: Kaiser Window
Up: Window Definitions
Previous: Lanczos Window
The Gaussian Window in its general form is defined by
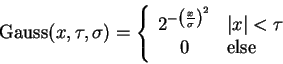 |
(12) |
with 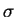 being the standard deviation. The higher
being the standard deviation. The higher 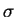 gets,
the wider gets the Gaussian window and, on the other hand, the more
severe gets the truncation. Several Gaussian windows with different
standard deviations are depicted in Fig. 2 in the
third row. The higher
gets,
the wider gets the Gaussian window and, on the other hand, the more
severe gets the truncation. Several Gaussian windows with different
standard deviations are depicted in Fig. 2 in the
third row. The higher 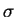 the better the frequency response
approximates the ideal one below
the better the frequency response
approximates the ideal one below 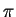 but also the more distinctive
are the bumps above
but also the more distinctive
are the bumps above 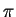 .
.
1999-04-08