
Next: Blackman Window
Up: Window Definitions
Previous: Parzen Window
The Hann (due to Julius van Hann, often wrongly referred to as Hanning
window [20], sometimes just cosine bell window) and
Hamming window are quite similar, they only differ in the choice of
one parameter 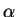 :
:
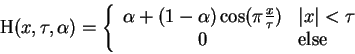 |
(9) |
with
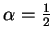 being the Hann window and
being the Hann window and 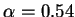 the
Hamming Window. The Hamming window also has the disadvantage of being
discontinuous at the edges (and has therefore a, however not so severe,
bump above
the
Hamming Window. The Hamming window also has the disadvantage of being
discontinuous at the edges (and has therefore a, however not so severe,
bump above 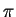 ), which leads to clearly visible artifacts in the
images.
), which leads to clearly visible artifacts in the
images.
1999-04-08