.
In the first step we add one vertex into the middle. The vertex is denoted by 
, where
Random midpoint displacement method introduced by Fouriner et al. [4] represents de facto standard in fractal terrains generation techniques. The principle is as follows.
An initial square is subdivided into four smaller squares (see Figure 2). Let us have four points
.
In the first step we add one vertex into the middle. The vertex is denoted by , where
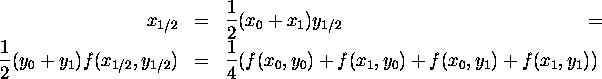
The added vertex is shifted in z-coordinate direction by random value denoted by 
.
This procedure is recursively repeated for each subsquare, then for every their descendants, and so on.
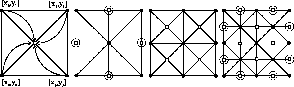
Figure 2: First four steps in random midpoint displacement method
In order to be resulting surface fBm, the random number 
must be generated with
Gaussian distribution
and in the i-th iteration step the variation 
have to be modified according
to
where H denotes Hurst exponent [6] ( 
). From equation (1)
we can see, that the first iteration has the biggest influence to the resulting shape of the
surface and influence of the others decreases.
In the second step we calculate the points on the edges of initial
square. We virtually rotate square by 
and calculate the values as in the previous step. The
problem is in the cases when the new point has just three neighbors (the encircled points in
Figure 2). In this case we calculate the average of three neighbors only. The error
produced on the border could be neglected.
In the next step we virtually rotate the square back by and we recursively apply the first two steps
on the four new squares as is mentioned above. This recursive process ends after given number of iteration.
Fractal dimension D of surface is obtained by
An example of fractal terrain obtained with random midpoint displacement algorithm is in Figure 3. The fractal dimension of this surface is D=2.5.
Figure: Example of fractal terrain with fractal dimension D=2.5. (a) wire frame model (b) the same model textured
